Презентация на тему: «Математические хитрости»
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:Неделя науки! Математические факты и хитрости. Подготовила: Барышникова М.А. учитель математики
2 слайд Описание слайда:Как легко умножить на 9 любое однозначное число Кладем перед собой собственные ладони. Загибаем тот палец, на какое число нужно умножить 9.
Среди всех фигур с одинаковым периметром, у круга будет самая большая площадь. И наоборот, среди всех фигур с одинаковой площадью, у круга будет самый маленький периметр.
Как возвести в квадрат двузначное число, оканчивающееся на 5 Для примера возьмем число 65. Умножаем количество его десятков на последующее число. Количество десятков – 6, следующее за шестёркой число – 7. Значит перемножаем шесть на семь: 6*7=42 Справа приписываем 25. Ответ: 4225. На самом деле, миг – это единица времени, которая длится примерно сотую долю секунды.
Число 18, является единственным (кроме нуля) числом, сумма цифр которого в два раза меньше него самого. В группе из 23-х человек и более, вероятность, что у двоих совпадет день рождения, превышает 50%, а в группе от 60 человек такая вероятность составляет около 99%. В математике существуют: теория кос, теория игр и теория узлов. Пирог можно разрезать тремя касаниями ножа на восемь равных частей. Причем, двумя способами. Ноль – единственное число, которое нельзя написать римскими цифрами.
В группе из 23-х человек и более, вероятность, что у двоих совпадет день рождения, превышает 50%, а в группе от 60 человек такая вероятность составляет около 99%. В математике существуют: теория кос, теория игр и теория узлов. Пирог можно разрезать тремя касаниями ножа на восемь равных частей. Причем, двумя способами. Ноль – единственное число, которое нельзя написать римскими цифрами.
Сумма чисел от 1 до 100 равняется 5050. С 1995-го года в Тайбэе, на Тайване, жителям разрешено удалять цифру четыре, так как на китайском языке эта цифра звучит тождественно слову «смерть». Во многих зданиях отсутствует четвертый этаж. Считается, что несчастливым число 13 стало из-за Тайной Вечери, на которой присутствовали 13 человек, включая Иисуса. 13-м был Иуда Искариот.
7 слайд Описание слайда:Первой женщиной-математиком в истории, считается гречанка Гипатия, жившая в египетской Александрии в IV-V веках нашей эры. В 1992-м году австралийские единомышленники объединились ради выигрыша в лотерею. На кону было 27 миллионов долларов. Количество комбинаций 6 из 44, составляло немногим более семи миллионов, при стоимости лотерейного билета в 1 доллар. Эти единомышленники создали фонд, в который каждый из 2500 человек вложил по три тысячи долларов. Результат – выигрыш и возврат 9 тысяч каждому.
В 1992-м году австралийские единомышленники объединились ради выигрыша в лотерею. На кону было 27 миллионов долларов. Количество комбинаций 6 из 44, составляло немногим более семи миллионов, при стоимости лотерейного билета в 1 доллар. Эти единомышленники создали фонд, в который каждый из 2500 человек вложил по три тысячи долларов. Результат – выигрыш и возврат 9 тысяч каждому.
Презентация к неделе математики в начальной школе «Математические хитрости»
Инфоурок › Математика ›Презентации›Презентация к неделе математики в начальной школе «Математические хитрости»Описание презентации по отдельным слайдам:
1 слайд Описание слайда:Математические хитрости
2 слайд Описание слайда: 3 слайд Описание слайда:5 13 20 27 6 14 21 28 7 15 22 29 1 8 16 23 30 2 9 17 24 3 10 18 25 4 11 19 26 24 47
4 слайд Описание слайда:Измерения Выберите предмет в комнате, который хотите измерить Используя два различных предмета, измерьте выбранный объект объект скрепки маркеры Дверь 147 13 Стол 85 5 Нога 12 1,5
Математика — это интересная игра не только цифрами, но и линиями. Не веришь? 1. Возьми лист бумаги прямоугольной формы или вырежи прямоугольник. 2. Начерти 10 одинаковых вертикальных линий, параллельных друг другу. 3. Далее проведи диагональ, как показано на рисунке.
Не веришь? 1. Возьми лист бумаги прямоугольной формы или вырежи прямоугольник. 2. Начерти 10 одинаковых вертикальных линий, параллельных друг другу. 3. Далее проведи диагональ, как показано на рисунке.
4. А теперь разрежь прямоугольник по диагонали. Его нижнюю часть сдвинь вниз. 5. Последним шагом перед Твоим удивлением будет подсчет количества вертикальных линий. Их стало 9!
7 слайд Описание слайда: 8 слайд Описание слайда:Вот такая вот математика! Недаром Феликс Хаусдорф сказал: «Есть в математике нечто, вызывающее человеческий восторг».
Математические стишки
10 слайд Описание слайда:Прочитай следующий цифровой шедевр и попробуй отгадать, стихи какого поэта в нем зашифрованы? 17 20 48 140 10 01 126 138 140 3 501
Это знаменитые строки Александра Пушкина из письма Татьяны Евгению Онегину: «Я к вам пишу — чего же боле? Что я могу еще сказать? Теперь, я знаю, в вашей воле Меня презреньем наказать…»
12 слайд Описание слайда:А в этом математическом стишке зашифрована песенка. Догадаешься, какая? 2 15 42 42 15 37 08 5 20 20 20! 7 14 100 0 2 00 13 37 08 5 20 20 20!
Догадаешься, какая? 2 15 42 42 15 37 08 5 20 20 20! 7 14 100 0 2 00 13 37 08 5 20 20 20!
Все просто! Это песня «Кабы не было зимы» из нашего любимого мультфильма «Зима в Простоквашино».
14 слайд Описание слайда:Следующий стих отгадать не сложно. Невероятно, насколько точно автор просчитал рифмы! 511 16 5 20 337 712 19 2.000.047 3 1.512 16.025 11 0 3 15 100.006 0 23
15 слайд Описание слайда:Догадались? Это стихотворение «Я помню чудное мгновенье» Александра Пушкина. «Я помню чудное мгновенье: Передо мной явилась ты, Как мимолетное виденье, Как гений чистой красоты. В томленьях грусти безнадежной, В тревоге шумной суеты, Звучал мне долго голос нежный И снились милые черты.»
В томленьях грусти безнадежной, В тревоге шумной суеты, Звучал мне долго голос нежный И снились милые черты.»
И, напоследок, предлагаю еще одно математическое произведение. 2 46 38 1 116 14 20 15 14 21 14017
17 слайд Описание слайда:Это «Стихи о Советском паспорте» Маяковского. «Я достаю из широких штанин Дубликат бесценного груза. Читайте, завидуйте, я — гражданин Советского Союза».
18 слайд Описание слайда: 19 слайд Описание слайда:Благодарю за внимание!
Методика быстрого счета без калькулятора
Цифры окружают нас с детства.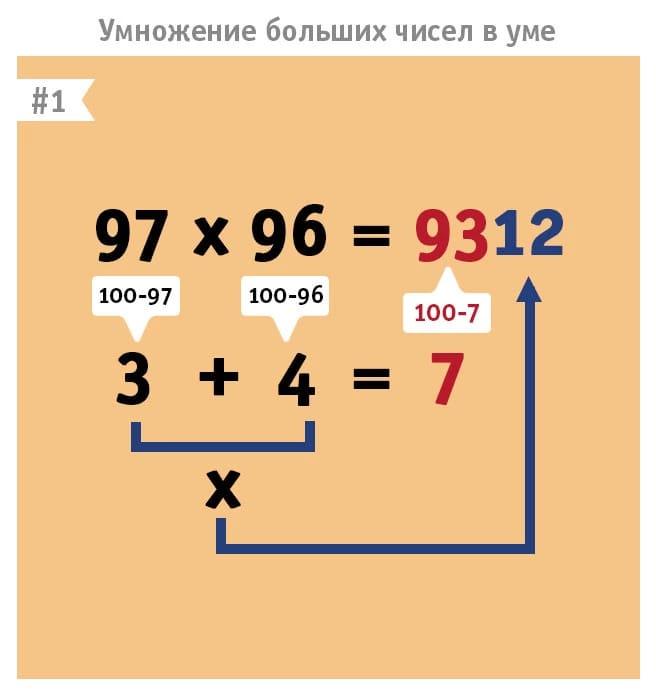 Еще до школы или в первом классе человек учится складывать и вычитать, решать простые примеры и задачи. Позже он осваивает таблицу умножения, переходя к более сложной части математических упражнений. Большинство людей может производить в уме только простые вычисления. А вот умножение и деление больших значений приходится выполнять на бумаге или с помощью калькулятора. Но можно ли как-то научиться хорошо считать без использования подручных средств?
Еще до школы или в первом классе человек учится складывать и вычитать, решать простые примеры и задачи. Позже он осваивает таблицу умножения, переходя к более сложной части математических упражнений. Большинство людей может производить в уме только простые вычисления. А вот умножение и деление больших значений приходится выполнять на бумаге или с помощью калькулятора. Но можно ли как-то научиться хорошо считать без использования подручных средств?
Быстрый счет без калькулятора
Жизнь любого современного человека неотрывно связана с числами. Без умения считать невозможно выполнять самые простые повседневные задачи. Конечно, сегодня у людей появились умные помощники – калькуляторы, смартфоны, компьютеры, но даже они могут иногда подвести – сломаться или не вовремя разрядиться. Да и не всегда можно полагаться на гаджеты, ведь на экзаменах в школе или в ВУЗе они не помогут. Именно поэтому многие люди стремятся научиться хорошо считать без помощи подручных средств. Особенно это актуально для школьников, ведь если с детства освоить техники быстрого устного счета, то и учеба в школе, и различные задачи во взрослой жизни будут даваться легче.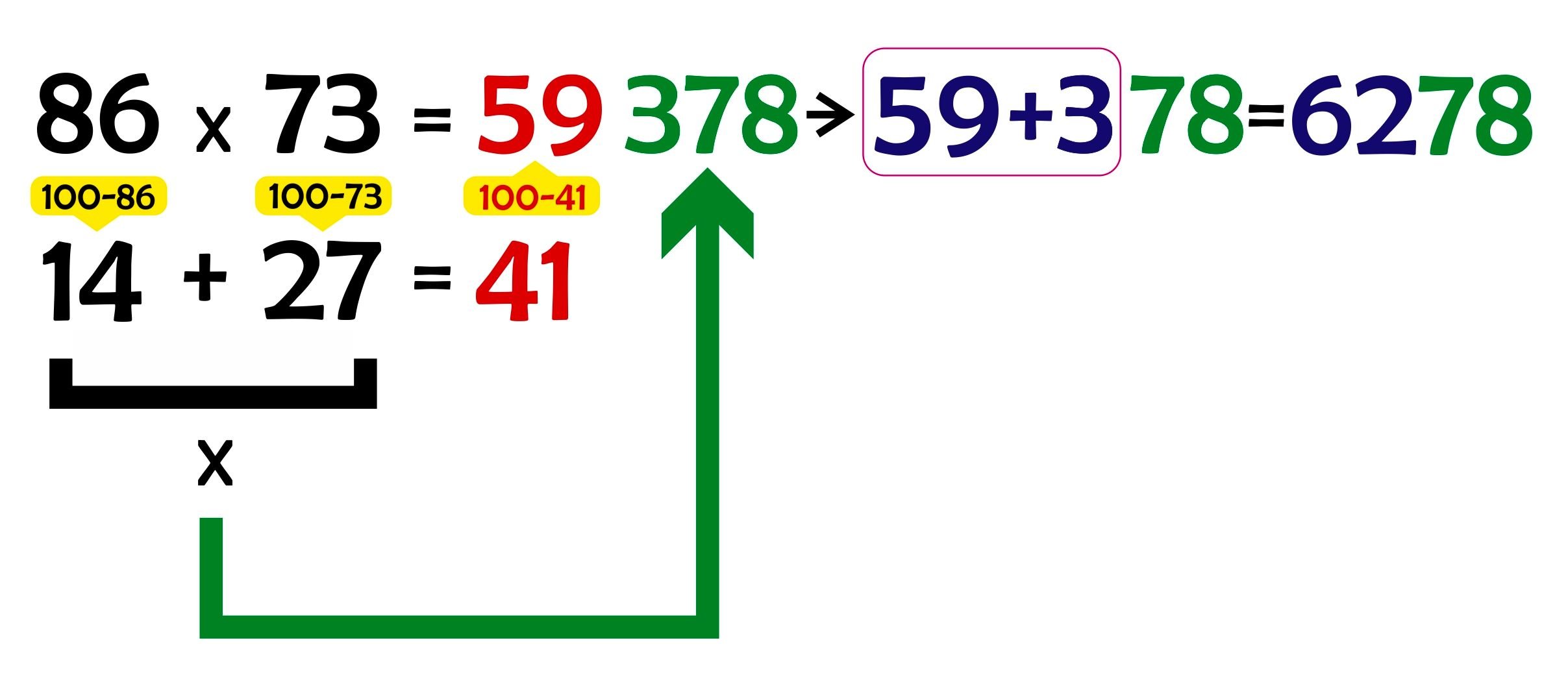
Есть еще одна серьезная причина для того, чтобы начать тренироваться хорошо считать в уме. Устный счет развивает человеческий мозг и способствует росту уровня интеллекта. Поэтому даже те студенты, которые обучаются на гуманитарных специальностях, все равно изучают такие точные науки, как высшая математика и математический анализ. Упражнения, направленные на устный счет больших чисел, являются отличной зарядкой для ума. Так развитие интеллекта и удобство в быту – это две самые главные причины научиться хорошо считать без калькулятора.
Человечество еще с древности стремилось найти такие способы быстрого счета. И речь не только о простых вычислениях, таких как сложение и вычитание, но и о более сложных – об умножении и делении. Пусть это и занимает много времени, но складывать и вычитать большие значения все же можно без предварительной подготовки, а вот такие действия, как умножение двузначных чисел, недоступны большинству людей.
Но, благодаря труду математиков со всего земного шара, сегодня появились некоторые математические хитрости, позволяющие считать в уме не только однозначные, но и двузначные числа. Чтобы понять принцип их работы, лучше рассмотреть каждый из этих приемов отдельно.
Чтобы понять принцип их работы, лучше рассмотреть каждый из этих приемов отдельно.
Популярная система быстрого счета
Существует несколько видов основных математических операций – сложение, вычитание, умножение и деление. И если с нахождением суммы и разности все более или менее понятно, то другие вычисления производить намного сложнее. Рассмотрим самые популярные математические хитрости, направленные на удобное умножение и деление в уме.
Умножение любого числа на 9
Решать устно такие примеры очень легко. Для этого достаточно умножить нужное значение на 10 и вычесть из получившегося ответа это же число. Например, нам нужно найти результат умножения 19 и 9. Пример будет выглядеть так: 19*10-19= 190-19=171. Этот прием достаточно легко применять на практике.
Умножение любого числа на 11
Похожим образом выглядит умножение любого значения на 11: мы находим произведение нашего числа и 10, а затем прибавляем к получившемуся выражению наше число. Допустим, мы ищем сколько будет 67*11, так у нас получается следующий пример: 67*10+67=670+67=737.
Допустим, мы ищем сколько будет 67*11, так у нас получается следующий пример: 67*10+67=670+67=737.
Умножение двузначного числа на однозначное
Проще всего производить такую операцию методом разбора множителей на десятки и единицы. Допустим, нам требуется перемножить 56 и 8. Для этого мы разделяем 56 на составные части, получается 50 и 6. Теперь мы отдельно перемножаем наши десятки и единицы на однозначное число и ищем их сумму. Получается 50*8+6*8=400+48=448. Но чем больше знаков в каждом из перемножаемых значений, тем сложнее производить подобные операции в уме.
Умножение двузначного числа на двузначное
Нахождение результата умножения двузначных чисел похоже на предыдущий метод. К примеру, необходимо найти произведение 24 и 52. Для этого мы разбиваем одно из чисел на десятки и единицы и перемножаем их на наш множитель, а затем складываем полученные выражения: 20*52+4*52=1040+208=1248. Чем больше каждое из чисел, тем сложнее находить результат умножения.
Нахождение процента от числа
Чтобы найти процент от любого значения, нужно умножить данное число на размер искомого процента и разделить на сто. Лучше рассмотреть данный подход на примере. Допустим, требуется найти 12% от 74. Мы производим умножение 12 и 74, разбирая это выражение на составные части. Получается 10*74+2*74=740+148=888. Теперь мы делим наш результат на 100 и получаем ответ – 8,88%. Так удается легко находить процент от любого значения без помощи калькулятора.
Деление многозначного числа на однозначное
Чтобы найти ответ на такой пример, нужно вспомнить таблицу умножения. Допустим, нам требуется разделить число 138 на 6. Для этого мы разбиваем делимое на части, получается 13 десятков и 8 единиц. Делим 13 на 6, получаем 2 и 1 в остатке. Это значит, что десятком в нашем ответе будет число 2. Остаток, а это 1 десяток, мы складываем с единицей делимого, получается 18. Делим 18 на 6, получается 3. Теперь складываем получившиеся десятки и единицы: 20+3=23.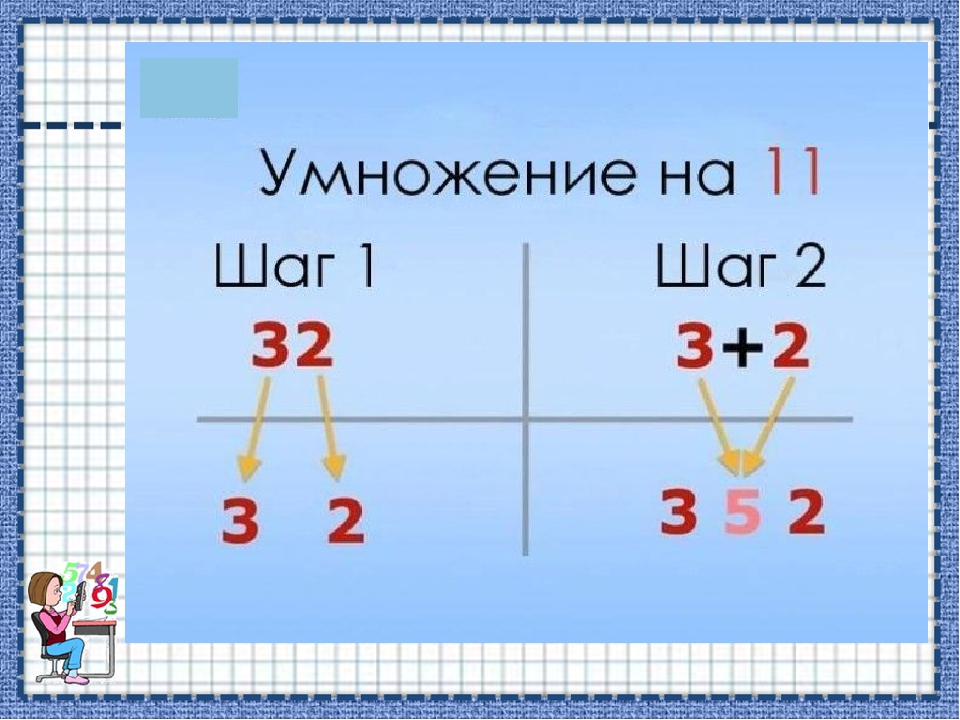 Целое выражение будет выглядеть так: 120/6+(10+8)/6=20+18/6=23.
Целое выражение будет выглядеть так: 120/6+(10+8)/6=20+18/6=23.
Существуют и другие, более сложные приемы устных математических вычислений, которые позволяют выполнять операции с многозначными числами. Но и освоить эти техники труднее, так как они требуют высокой концентрации и хорошо развитой памяти.
К плюсам всех подобных приемов можно отнести уже то, что такому счету можно научиться достаточно быстро. Перечисленные способы имеют множество вариаций от простых до более сложных, поэтому некоторые из них охотно используют даже дети. Но все эти методы имеют один существенный недостаток, который не позволяет им называться полноценной системой счета в уме.
Такие способы вычислений подразумевают соблюдение целого ряда условий. Например, правила для умножения трехзначных чисел отличаются от правил для двузначных. Поэтому приходится запоминать большое количество условий, чтобы можно было применять в быту такие способы счета. Все это делает подобные методы сложения, вычитания, умножения и деления скорее зарядкой для ума, чем продуктивным подходом к вычислениям.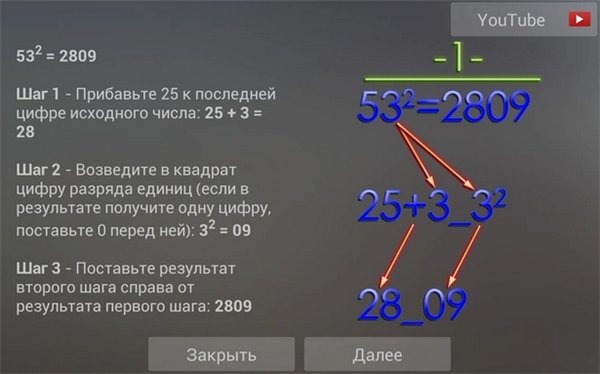
Но существуют и кардинально иные техники, позволяющие развить навыки человека и научиться очень хорошо считать без подручных средств. Одной из самых популярных методик быстрого устного счета является ментальная арифметика. Рассмотрим ее преимущества подробнее.
Как научить ребенка считать в уме
Ментальная арифметика – это далеко не новая система быстрого счета, ведь она зародилась еще в древности, около пяти тысяч лет назад. С тех пор данная методика не претерпела серьезных изменений и дошла до нас в практически первозданном виде. В ее основе лежат вычисления на абакусе – специальных счётах. Сначала человек учится решать простейшие примеры на них, а затем постепенно переходит к более сложному этапу обучения – учится представлять абакус в уме и производить вычисления на нем в своем воображении.
Лучше всего ментальная арифметика подходит именно детям. Нет, взрослые также могут ее освоить, но для этого им придется абстрагироваться от привычных методов операций с числами, а ребенок справляется с этим намного легче. Для него ментальная арифметика является не только помощником на уроках математики, но и способом развить свои интеллектуальные способности до очень высокого уровня.
Весь секрет этой методики в том, что она подразумевает разностороннее развитие человека. За логику и анализ отвечает правое полушарие мозга, именно оно задействуется на обычных уроках математики, когда мы решаем примеры или задачи. Правое полушарие, отвечающее за креативное мышление и фантазию, в этом случае к работе почти не подключается, а значит и не развивается должным образом. А ведь все области человеческого интеллекта необходимо тренировать.
Так как ментальная арифметика задействует и аналитическое мышление, и воображение, она является даже не столько способом быстро решать математические задачи, сколько средством для всестороннего развития. Другие методики чаще всего направлены на тренировку какой-то одной способности, а данная техника работает комплексно. Именно это выделяет ее среди прочих и делает одной из самых популярных систем развития интеллекта ребенка.
Обучение ментальной арифметике занимает достаточно много времени, но те преимущества, которые она дает, оправдывают затраченные усилия. Когда речь идет об обучении ребенка по данной методике, важно подобрать правильную программу тренировок. Ключевым фактором успеха является соблюдение плана занятий и контроль их регулярности. Несмотря на то, что в открытых источниках в интернете можно найти много информации по этому запросу, не всегда удается самостоятельно освоить ментальную арифметику. Поэтому большинство родителей предпочитают обучать ребенка этой технике в детских центрах дополнительного образования.
Как выбрать эффективную методику
Сегодня многие учебные заведения предлагают пройти курсы ментальной арифметики. Но детское образование – это очень сложный и многогранный процесс, поэтому родители должны походить к нему внимательно, и выбирать такие занятия, которые точно принесут пользу.
Выбирая школу ментальной арифметики, обращайте внимание на то, чтобы обучение велось по проверенной методике и учитывало возрастные особенности каждого ребенка. Нельзя, чтобы в одной группе обучались дети из начальной школы и старшеклассники, ведь в каждом возрасте своя скорость освоения, запоминания и закрепления материала.
К тому же, маленьким детям лучше всего преподавать любой предмет в игровой форме. Так они не будут уставать учиться и смогут сохранять концентрацию в течение всего урока. Внедрение игры в образовательный процесс способствует повышению интереса ребенка к математике.
Очень важно, чтобы тренер успевал уделить внимание каждому ученику в процессе занятия, но это возможно только в небольших группах. Поэтому стоит отдавать предпочтение тем детским центрам, где педагог обучает не более десяти детей единовременно. Только тогда удастся заниматься с максимальной продуктивностью.
Если учебный план организован правильно, то ребенку удастся приобрести полезные навыки, благодаря которым математика станет для него интересным и любимым предметом. Все это положительно скажется на успеваемости в школе, ведь, когда учеба дается легко, заниматься намного веселее.
Все это делает обучение ментальной арифметике самым продуктивным способом освоения быстрого устного счета.Ребенку больше не придется прибегать к различным математическим хитростям, чтобы легко справляться с задачами и примерами. Ученик приобретает навыки, которые сохраняются на всю жизнь, а значит они пригодятся ему не только в учебе, но и в карьерной деятельности. Все это делает обучение данной технике отличным вкладом в будущее своего ребенка.
Приёмы устного счета для быстрого вычисления в уме
Зачем считать в уме, если решить любую арифметическую задачу можно на калькуляторе. Современная медицина и психология доказывают, что устный счет — это тренаж для серых клеточек. Выполнять такую гимнастику необходимо для развития памяти и математических способностей.
Известно множество приёмов для упрощения вычислений в уме. Все, кто видел знаменитую картину Богданова-Бельского «Устный счёт», всегда удивляются — как крестьянские дети решают такую непростую задачу, как деление суммы из пяти чисел, которые предварительно ещё надо возвести в квадрат?
Оказывается, эти дети — ученики известного педагога-математика Сергея Александровича Рачицкого (он также изображен на картине). Это не вундеркинды — ученики начальных классов деревенской школы XIX века. Но все они уже знают приёмы упрощения арифметических расчетов и выучили таблицу умножения! Поэтому решить такую задачку этим детишкам вполне под силу!
Секреты устного счёта
Существуют приемы устного счета — простые алгоритмы, которые желательно довести до автоматизма. После овладения простыми приёмами можно переходить к освоению более сложных.
Прибавляем числа 7,8,9
Для упрощения вычислений числа 7,8,9 сначала надо округлять до 10, а затем вычитать прибавку. К примеру, чтобы прибавить 9 к двузначному числу, надо сначала прибавить 10, а затем вычесть 1 и т.д.
Примеры:
56+7=56+10-3=63
47+8=47+10-2=55
73+9=73+10-1=82
Быстро складываем двузначные числа
Если последняя цифра двузначного числа больше пяти, округляем его в сторону увеличения. Выполняем сложение, из полученной суммы отнимаем «добавку».
Примеры:
54+39=54+40-1=93
26+38=26+40-2=64
Если последняя цифра двузначного числа меньше пяти, то складываем по разрядам: сначала прибавляем десятки, затем — единицы.
Пример:
57+32=57+30+2=89
Если слагаемые поменять местами, то сначала можно округлить число 57 до 60, а потом вычесть из общей суммы 3:
32+57=32+60-3=89
Складываем в уме трехзначные числа
Быстрый счет и сложение трехзначных чисел — это возможно? Да. Для этого надо разобрать трехзначные числа на сотни, десятки, единицы и поочередно их приплюсовать.
Пример:
249+533=(200+500)+(40+30)+(9+3)=782
Особенности вычитания: приведение к круглым числам
Вычитаемые округляем до 10, до 100. Если надо вычесть двузначное число, надо округлить его до 100, вычесть, а затем к остатку прибавить поправку. Это актуально если поправка невелика.
Примеры:
67-9=67-10+1=58
576-88=576-100+12=488
Вычитаем в уме трехзначные числа
Если в свое время был хорошо усвоен состав чисел от 1 до 10, то вычитание можно производить по частям и в указанном порядке: сотни, десятки, единицы.
Пример:
843-596=843-500-90-6=343-90-6=253-6=247
Умножить и разделить
Моментально умножать и делить в уме? Это возможно, но без знания таблицы умножения не обойтись. Таблица умножения — это золотой ключик к быстрому счету в уме! Она применяется и при умножении, и при делении. Вспомним, что в начальных классах деревенской школы в дореволюционной Смоленской губернии (картина «Устный счет») дети знали продолжение таблицы умножения — с 11 до 19!
Хотя на мой взгляд достаточно знать таблицу от 1 до 10, чтобы мочь перемножать бо´льшие числа. Например:
15*16=15*10+(10*6+5*6)=150+60+30=240
Умножаем и делим на 4, 6, 8, 9
Овладев таблицей умножения на 2 и на 3 до автоматизма, сделать остальные расчеты будет проще простого.
Для умножения и деления двух- и трехзначных чисел применяем простые приёмы:
-
умножить на 4 — это дважды умножить на 2;
-
умножить на 6 — это значит умножить на 2, а потом на 3;
-
умножить на 8 — это трижды умножить на 2;
-
умножить на 9 — это дважды умножить на 3.
Например:
37*4=(37*2)*2=74*2=148;
412*6=(412*2)·3=824·3=2472
Аналогично:
-
разделить на 4 — это дважды разделить на 2;
-
разделить на 6 — это сначала разделить на 2, а потом на 3;
-
разделить на 8 — это трижды разделить на 2;
-
разделить на 9 — это дважды разделить на 3.
Например:
412:4=(412:2):2=206:2=103
312:6=(312:2):3=156:3=52
Как умножать и делить на 5
Число 5 — это половина от 10 (10:2). Поэтому сначала умножаем на 10, затем полученное делим пополам.
Пример:
326*5=(326*10):2=3260:2=1630
Еще проще правило деления на 5. Сначала умножаем на 2, а затем полученное делим на 10.
326:5=(326·2):10=652:10=65,2.
Умножение на 9
Чтобы умножить число на 9, необязательно его дважды умножать на 3. Достаточно его умножить на 10 и вычесть из полученного умножаемое число. Сравним, что быстрее:
37*9=(37*3)*3=111*3=333
или
37*9=37*10 — 37=370-37=333
Также давно замечены частные закономерности, которые значительно упрощают умножение двузначных чисел на 11 или на 101. Так, при умножении на 11, двузначное число как бы раздвигается. Составляющие его цифры остаются по краям, а в центре оказывается их сумма. Например: 24*11=264. При умножении на 101, достаточно приписать к двузначному числу такое же. 24*101= 2424. Простота и логичность таких примеров вызывает восхищение. Встречаются такие задачи очень редко — это примеры занимательные, так называемые маленькие хитрости.
Счет на пальцах
Сегодня еще можно встретить много защитников «пальчиковой гимнастики» и методики устного счета на пальцах. Нас убеждают, что учиться складывать и отнимать, загибая и разгибая пальцы — это очень наглядно и удобно. Диапазон таких вычислений очень ограничен. Как только расчеты выходят за рамки одной операции возникают трудности: надо осваивать следующий прием. Да и загибать пальцы в эпоху айфонов как-то несолидно.
Например, в защиту «пальчиковой» методики приводится приём умножения на 9. Хитрость приёма такова:
- Чтобы умножить любое число в пределах первой десятки на 9, надо развернуть ладони к себе.
- Отсчитывая слева направо, загнуть палец, соответствующий умножаемому числу. К примеру, чтобы умножить 5 на 9, надо загнуть мизинец на левой руке.
- Оставшееся количество пальцев слева будет соответствовать десяткам, справа — единицам. В нашем примере — 4 пальца слева и 5 справа. Ответ: 45.
Да, действительно, решение быстрое и наглядное! Но это — из области фокусов. Правило действует только при умножении на 9. А не проще ли, для умножения 5 на 9 выучить таблицу умножения? Этот фокус забудется, а хорошо выученная таблица умножения останется навсегда.
Также существует еще множество подобных приемов с применением пальцев для каких-то единичных математических операций, но это актуально пока вы этим пользуетесь и тут же забывается при прекращении применения. Поэтому лучше выучить стандартные алгоритмы, которые останутся на всю жизнь.
Устный счёт на автомате
-
Во-первых, необходимо хорошо знать состав числа и таблицу умножения.
-
Во-вторых, надо запомнить приемы упрощения расчётов. Как выяснилось, таких математических алгоритмов не так уж много.
-
В-третьих, чтобы приём превратился в удобный навык, надо постоянно проводить краткие «мозговые штурмы» — упражняться в устных вычислениях, используя тот или иной алгоритм.
Тренировки должны быть короткими: решить в уме по 3-4 примера, используя один и тот же приём, затем переходить к следующему. Надо стремиться использовать любую свободную минутку — и полезно, и нескучно. Благодаря простым тренировкам все вычисления со временем будут совершаться молниеносно и без ошибок. Это очень пригодится в жизни и выручит в непростых ситуациях.
крутых математических уловок, чтобы удивить ваших друзей
крутых математических уловок с использованием 1Математика похожа на волшебство, только лучше! Вот набор классных математических приемов, которым вы можете научиться, чтобы удивить своих друзей и узнать больше о том, как работают числа.
Правило 11
Всем известно «Правило 10», где вы умножаете на 10, просто прибавляя 0 к концу числа, но вы можете не знать правила 11. Это правило работает для любого двузначного числа, чтобы умножить его на 11:
. Например, давайте использовать число 62
- . Разделите две цифры в уме (6 __ 2).
- Сложите две цифры чисел. (6 + 2 = 8).
- Поместите это число в пробел или дыру между двумя цифрами (6 8 2).
- Вот и все! 11 x 62 = 682
Единственная сложная часть, которую следует запомнить, заключается в том, что если сложение двух цифр приводит к числу больше 9, то вы помещаете цифру «единицы» в пробел и переносите цифру «десятки». Например:
11 x 57… 5 __ 7… 5 + 7 = 12
, поэтому вы помещаете 2 в пробел и добавляете 1 к 5, получая число 627
11 x 57 = 627
Обратный отсчет Математический приемОднозначные числа Математический прием
- Подумайте о двухзначных числах.
- Возьмите любое из чисел и удвойте его.
- Добавьте 5 к результату.
- Добавьте второе число к своему ответу.
- Вычтите 25 из ответа.
- В ответе вы получите 2 однозначных числа.
Использование размера обуви для определения вашего возраста — алгебраический трюк
Есть много математических приемов, которые просят вас указать число, чтобы получить «скрытый» номер, который вы фактически вводите в другой форме во время трюка. Первое число не слишком важно, так как оно удаляется во время трюка, поэтому вы можете изменить формулировку этого математического трюка.
- Определите свой возраст по размеру обуви. Возьмите размер обуви (целое число, округлите, если он половинный).
- Умножьте его на 5.
- Добавьте 50.
- Умножьте на 20.
- Добавьте 1016. (если вы проделываете фокус в 2016 году… если это 2017 год, используйте 1017, в 2018 используйте 1018 и т. Д. )
- Вычтите год своего рождения.
- Первая цифра — это размер вашей обуви, а последние две цифры — ваш возраст.
Как вы могли догадаться, этот трюк предназначен для выявления числа, которое меньше 100.Уловка использует алгебру для поиска ответа. Давайте сделаем трюк еще раз, используя s для размера обуви и b для года рождения:
Умножить sx 5: 5s
Добавить 50: 5s + 50
Умножить на 20:20 (5s + 50) = 100s + 1000
Добавить 1016 (в зависимости от текущего года): 100 с + 1000 + 1016 = 100 с + 2016
Вычесть год рождения: 100 с + 2016 — b
Почему это работает (и почему иногда не работает)? Независимо от размера вашей обуви, это будут первые две цифры ответа.Если ваш размер обуви 9, 100 — это 900. Если вы используете европейскую таблицу размеров и носите размер 36, то 100 = 3600.
В возрастной части берется текущий год минус год вашего рождения. Уловка не учитывает месяц вашего рождения, поэтому, если ваш день рождения в этом году не наступил, ответ будет через год!
1, 2, 4, 5, 7, 8 Математический трюк
- Выберите число от 1 до 6.
- Умножьте число на 9.
- Умножьте результат на 111.
- Умножьте ответ на 1001.
- Разделите число на 7.
- Ответ будет содержать все числа 1, 2, 4, 5, 7, 8.
Совет запомнить Пи
Пи — иррациональное число, поэтому вы не можете узнать все его цифры. Однако вы можете изучить первые несколько для расчетов. Просто запомните фразу:
«Как бы я хотел вычислить пи».
Количество букв в каждом слове — это цифра, что дает вам 3,141592.
Математический трюк 1089
- Подумайте о трехзначном числе.
- Расположите цифры в порядке убывания.
- Поменяйте порядок ответов на обратный и вычтите его из числа на шаге 2.
- Поменяйте порядок ответов на обратный.
- Добавьте его к результату шага 3. Вы получите 1089!
- Например, я выбрал 423.
- Расположите в порядке убывания: 432
- Поменяйте порядок в обратном порядке и вычтите его из предыдущего числа: 234… 432 — 234 = 198
- Переверните порядок: 891
- Сложите числа: 198 + 891 = 1089
- Например, число 245.
- В порядке убывания это 542.
- В обратном порядке это 245.
- 542 — 245 = 297
- В обратном порядке, это 792
- 792 + 297 = 1089
Ответ 5
- Подумайте о число.
- Удвойте.
- Сложите 10.
- Разделите на 2.
- Вычтите исходное число.
- Ваш ответ — 5!
Ответ: 2
- Придумайте число.
- Умножьте на 3.
- Добавьте 6 к своему ответу.
- Разделите новое число на 3.
- Вычтите исходное число из этого.
- Ответ: 2.
- Например, число 2345.
- Если умножить на 3, получится 7035.
- Сложение 6 дает 7041.
- Деление на 3 дает 2347.
- Вычитание оригинала: 2347 — 2347 = 2.
Три цифры — один и тот же трюк
- Представьте себе трехзначное число, в котором все цифры одинаковы (например,г., 333, 777).
- Сложите цифры.
- Разделите ваше трехзначное число на добавленную стоимость.
- Ваш ответ 37.
Умножение на 6
Всякий раз, когда вы умножаете 6 на четное число, последняя цифра в ответе будет такой же, а цифра в разряде десятков будет половина цифры в единицах место.
Пример : 6 x 8 = 48
Математическая загадка о дне рождения ШерилКак решить математическую загадку о дне рождения Шерил
«День рождения Шерил» — это скорее математическая загадка или логическая головоломка, которая решается с помощью процесса исключения или дедуктивное мышление.Альберт не может знать день рождения, потому что у него есть только месяц, а у всех месяцев есть несколько дат, но у него достаточно информации, чтобы знать, что Бернар не знает даты. Если бы Шерил сказала Бернарду 19 или 18, он бы знал день рождения целиком, потому что каждое число содержит только один месяц. Это исключает 19 мая и 18 июня.
Поскольку Альберт знает, что Бернар не знает, Альберту, должно быть, сказали в июле или августе, поскольку это исключает любую возможность того, что Бернарду скажут 18 или 19. Это исключает любые даты в мае или Июнь.
Когда Бернар говорит, что не знал ответа, но теперь он знает, это означает, что у Бернарда есть единственный оставшийся уникальный номер в списке. Если бы у Бернарда было 14, он бы не знал, июль это или август. Если бы у него было 15 или 17, он бы не знал, какая дата в августе правильная. Таким образом, день рождения Шерил должен быть 16 июля!
Если вы хотите по-настоящему хитрить, вы можете перефразировать загадку, сказав, что Бернард начинает с того, что он не знает, когда наступит день рождения, на что Альберт отвечает, что он тоже не знает.Если Бернард тогда говорит, что не знал, а теперь знает, и Альберт отвечает, что теперь он тоже знает, то ответ — 17 августа. Вы понимаете, почему?
Есть ли у вас другие интересные математические уловки? Отправьте ответ и поделитесь ими!
Похожие сообщения
प्रतियोगी गणित के सभी अध्याय
प्रतियोगी गणित के इस पेज़ पर आपको मिलेंगी सबसे बेहतरीन ट्रिक्स, ये ट्रिक्स खास तौर पर सभी प्रतियोगी परीक्षाओं में रखकर यहाँ सँजोयी, आपको देखने को मिलेंगे वो वास्तव में रहे हैं और हर बार पूछे जाते हैं अगर आप अच्छे से प्रैक्टिस कर लेते होने से कोई नहीं रोक सकता!
Математические приемы के इस Страница पर आपको सबसे बेहतर ट्रिक्स मिलेंगी, यहाँ आपको Математические приемы, математические сокращения, बहुत ही आसान भाषा में समझाया गया है | ये Математические приемы सभी प्रतियोगी परीक्षाओं जैसे SSC CGL, SSC CHSL, Банковские экзамены, Железная дорога, भी सभी प्रतियोगी परीक्षाओं के लिए बेहद उपयोगी हैं |
सबसे नीचे पढ़ें “ एसएससी सीजीएल के की तैयारी कैसे करें “
Обновлено — 05 июля 2020 г.
क्रम इस प्रकार है — 1.Главы — 2. Загрузки
1. Главы (Математические приемы на хинди)
- औसत (СРЕДНИЙ) — (20+ коротких приемов)
- कैसे ज्ञात करें ईकाई का अंक
- अनुपात एवं समानुपात के 24 सबसे महत्वपूर्ण सवाल
- संख्या पद्धति के महत्वपूर्ण प्रश्न एवं शॉर्ट ट्रिक्स
- संख्या पद्धति के ये प्रश्न ऐसे ही पूछे जाते हैं! 2
- पद्धति | भाग — 3
- संख्याओं के योग से बनने वाले प्रश्न [Короткие трюки]
- घातांक एवं करणी के 30 महत्वपूर्ण सवाल
- प्रतिशत के 19 सबसे महत्वपूर्ण सवाल बार बार पूछे जाते हैं!
- LCM तथा HCF से अक्सर पूछे जाने वाले प्रश्न तथा उनके हल (Уловки LCM и HCF на хинди)
- बट्टा के 32 सबसे महत्वपूर्ण सवाल (Уловки со скидочными вопросами на хинди)
- लाभ और हानि के 35 सवाल जिनमें से हर बार सवाल
- के 23 महत्वपूर्ण सवाल
- वर्गमूल तथा घनमूल के 20 जबरदस्त सवाल
- सरलीकरण के इन 30 सवालों मेंं 1 सवाल हमेशा परीक्षा में आता है !!
- साधारण ब्याज के 16 सबसे महत्वपूर्ण सवाल
- ब्याज (भाग -1) (Вопрос о сложном проценте на хинди)
- चक्रवृध्दि ब्याज (भाग -2) (Вопрос о сложном проценте на хинди)
- चक्रवृध्दि ब्याज (भाग -3) (Вопрос о сложном проценте на хинди)
- कार्य तथा समय के ये 15 सवाल हैं सबसे जरूरी। हर परीक्षा में पूछे जाते हैं।
- आयु पर आधरित प्रश्न (Вопрос основан на возрасте на хинди с уловкой)
- मिश्रण- Решение с помощью коротких приемов (смешанный вопрос на хинди)
- समय तथा दूरी के 11 सबसे महत्वपूर्ण सवाल
- नल एवमं हौज़ (Короткие приемы ) -Часть-1
- नल एवं हौज с короткими трюками (Часть-2)
- रेलगाडी से सम्बंधित प्रश्न भाग -1 (Вопрос, связанный с железной дорогой на хинди)
- रेलगाडी सम्बंधित प्रश्न भाग -2 (Вопрос, связанный с железной дорогой на хинди )
- नाव तथा धारा — सम्बंधित प्रश्न (Вопрос о лодке и ручье на хинди)
- ऊंचाई और दूरी — Часть 1 (Вопросы о высоте и расстоянии на хинди)
- ऊंचाई और दूरी — भाग 2 (Вопросы о высоте и расстоянии на хинди)
- ऊंचाई और दूरी — भाग 3 (вопросы о высоте и расстоянии на хинди)
- त्रिभुज के ये 20 प्रमेय तथा तथ्य आपको आने चाहिये
- चतुर्भुज (четырехугольник) से सम्बंधित अतिमहत्वपूर्ण तथ्य व प्रमेय
- वृत्त से सम्बंधित महत्वपूर्ण प्रमेय | परीक्षा के लिये बेहद आवश्यक
- बीजगणित के बेहद महत्वपूर्ण सवाल 1
- बीजगणित के बेहद महत्वपूर्ण सवाल 2
- बीजगणित के बेहद महत्वपूर्ण सवाल 3
- बीजगणित के बेहद महत्वपूर्ण सवाल 4
- बीजगणित के बेहद महत्वपूर्ण सवाल 5
- त्रिकोणमिति के बेहद महत्वपूर्ण सवाल भाग 1
- त्रिकोणमिति के बेहद महत्वपूर्ण सवाल भाग 2
- त्रिकोणमिति के बेहद महत्वपूर्ण सवाल भाग 3
- त्रिकोणमिति के बेहद महत्वपूर्ण सवाल भाग भाग 4
- त्रिकोणमिति के बेहद महत्वपूर्ण सवाल भाग 5
- त्रिकोणमिति के बेहद महत्वपूर्ण सवाल भाग 6
- त्रिकोणमिति के बेहद महत्वपूर्ण सवाल भाग 7
- त्रिकोणमिति के बेहद महत्वपूर्ण सवाल भाग 8
Загрузки (математические приемы на хинди)
- Алгебра, рукописные заметки на хинди PDF Загрузить
- Abhinay Maths Class Notes PDF | Ссылки на Google Диск
- चक्रवृद्धि ब्याज हल करने का सबसे आसान तरीका Рукописные заметки
- 230 Вопросы о геометрии на хинди и английском Скачать PDF | С теоремой
- Геометрия के 198, बार पूछे गये प्रश्न एवं हल
- औसत (Среднее) के 100
Удивительный математический трюк 234X = ??? Уловка! Уловка!
Презентация на тему: «Удивительный математический трюк 234X234 + 1234-875 = ??? Уловка! Уловка!» — стенограмма презентации:
1 Удивительный математический трюк 234X = ??? Уловка! Уловка!
2 Хитрость! Этот трюк заставляет вас выглядеть так, будто ваш мозг — мега быстрый калькулятор! Попросите друга записать ЛЮБОЕ трехзначное число, например 231 или 884.Попросите их умножить число на x 7 x 11 x 13 … но даже если ваш друг пользовался калькулятором, вы уже давно записали ответ! Это дьявольски! СЕКРЕТ: все, что вам нужно сделать, это дважды выписать стартовый номер! Итак, 231 станет, а 884 станет. Вы не верите? Ну попробуйте на этом калькуляторе и убедитесь в этом сами! Вы работаете с этим калькулятором, щелкая мышью по кнопкам. Продолжайте, введите ЛЮБОЕ трехзначное число, затем x7 x11 x 13 и посмотрите, что вы получите!
3 Уловка 3367: эта уловка похожа на уловку.Это сложнее сделать, но выглядит намного чудеснее! Попросите друга выбрать любое двухзначное число, например 74 x 3367 Чтобы выработать окончательный ответ, вы должны представить себе исходное число, записанное три раза, например, затем разделить его на три. Это требует практики, но, в отличие от других, очень трудно понять, как это делается!
4 Уловка MISSING DIGIT!
Вот оно! Пойдите и спрячьтесь в шкафу или прикройте глаза каким-нибудь образом, чтобы не видеть, что пишет ваш друг.Попросите друга тайно записать ЛЮБОЙ номер (не менее четырех цифр). например, попросите друга сложить цифры … например = 23 … а затем вычтите ответ из первого числа. например = 78318 Ваш друг затем вычеркнул ОДНУ цифру из ответа. (Это может быть любая цифра, кроме нуля), например. 7×318 Ваш друг затем зачитывает оставшиеся цифры. Например, даже если вы не видели никаких цифр, вы можете сказать, какая цифра отсутствует! СЕКРЕТНО ВОСЕМЬ Этот замечательный трюк основан на силе числа 9. После того, как ваш друг сложит цифры и вычтет их, ответ ВСЕГДА будет делиться на 9.Если число делится на девять, то, когда вы складываете цифры, они также делятся на 9. Если вы проверите наш пример = 27, который действительно делится на девять. Когда ваш друг вычеркивает цифру, он затем зачитывает оставшиеся цифры. Вы их складываете. В нашем примере было = 19. Все, что вам теперь нужно сделать, это посмотреть, что нужно добавить к своему ответу, чтобы получить следующее число, которое делится на девять! Следующее число, которое нужно разделить на 9 после 19, — 27. Итак, вам нужно добавить ВОСЕМЬ. Это число, которое было вычеркнуто!
5 Уловка с днем рождения Эта математическая уловка определит ваш день рождения.Просто следуйте инструкциям на калькуляторе и нажимайте равно после каждого шага. Идите вперед и попробуйте трюк без обмана! Чтобы получить простой онлайн-калькулятор JavaScript, нажмите кнопку калькулятора. 1. Добавьте 18 к месяцу вашего рождения 2. Умножьте на 25 3. Вычтите 333 4. Умножьте на 8 5. Вычтите 554 6. Разделите на 2 7. Добавьте дату вашего рождения 8. Умножьте на 5 9. Добавьте 692 10. Умножьте на 20 11. Добавьте только две последние цифры года вашего рождения 12. Вычтите, чтобы получить свой день рождения! Формат ответа: месяц / день / год.Например, ответ означает, что вы родились 31 декабря. Если ответ неправильный, вы неправильно следовали инструкциям или солгали о своем дне рождения.
6 Тайна «24»! Поклонник убийственной математики по имени OBAID заметил, что если возвести в квадрат ЛЮБОЕ простое число больше 3, а затем вычесть 1, ответ всегда делится на 24! Например. 112 = 121, тогда = 120 и да, 120 делится на 24. ПОЧЕМУ? Если вы разбираетесь в алгебре (и читали «Призрак X»), то вы знаете, что все простые числа можно записать как (6n + 1) или (6n-1).(6n + 1) 2 = 36n + 12n + 1. Итак, (6n + 1) 2-1 = 36n + 12n. Это фабрики до 12n (3n + 1). Либо n, либо (3n + 1) должны быть четными, поэтому все выражение должно делиться на 24. (6n-1) 2 = 36n-12n + 1. Итак (6n-1) 2-1 = 36n-12n. Это заводов до 12н (3н-1). Либо n, либо (3n-1) должны быть четными, поэтому все выражение должно делиться на 24.
7 Уловка с простыми числами Используя простые числа, вы можете удивить своих друзей предсказанием простых чисел… Попросите друзей выбрать любое простое число больше 5, но они не должны говорить вам, что это такое. Выровняйте это. (Другими словами, умножьте простое число само на себя.) Сложите 17 Разделите на 12 Не зная, какое простое число выбрали ваши друзья, вы все равно можете сказать им: остаток будет 6. Например, если вы хотите попробовать этот трюк с простым числом 2801, вот что нужно нажать: 2801 * 2801 = = / 12 = … и вот ответ! Теперь найдите новое простое число и попробуйте его.
8 УДИВИТЕЛЬНЫЙ МАТЕРИАЛ 1999 ГОДА
1.Прежде всего, выберите количество дней в неделю, в которые вы хотите есть вне дома. 2. Умножьте это число на 2. 3. Добавьте 5. 4. Умножьте на 50. 5. Если в этом году у вас уже был день рождения. . . прибавьте 1749. Если в этом году у вас еще не было дня рождения. . . сложите 1748. 6. Последний шаг: вычтите четырехзначный год вашего рождения. Теперь у вас должно получиться трехзначное число: первая цифра этого номера была вашим исходным числом (т.е. сколько раз вы хотите ходить в ресторан каждую неделю). Вторые две цифры — ваш возраст !!! Это единственный год, который когда-либо будет работать, так что развлекайтесь, пока он длится.. .
9 Уловка с телефонным номером.