100 к 1 кто всех умнее ответ: 100 к 1 — ответы на все вопросы! — Stevsky.ru

100 к 1 — ответы на все вопросы! — Stevsky.ru

02.12.2013 18:03 Онлайн игры — Игры вконтакте

Сто к одному

Игра 100 к 1 сегодня стала весьма популярной в социальных сетях в Контакте и в Одноклассниках, это приложение установили уже около 5 000000 геймеров со всего мира.  Игратьв 100 к 1 можно и на других специализированных сайтах. Да, игра сто к одному не претендует на звание лучшего геймплея или прорыва в графике. Это простая реализация занимательной викторины, которая заслуживает внимания каждого поклонника оригинальной телепрограммы.
Приложение 100 к 1 реализовано по сценарию известного телешоу «Сто к одному», однако правила отличаются от оригинала. Викторина имеет достаточно простые правила – вам необходимо ответить на предлагаемые вопросы к игре 100 к 1. Раунды проходят с участием двух геймеров. За правильные

ответы к игре 100 к 1вам даются призовые очки. В случае, если вопрос простой, то и баллов вы получите меньше, чем за верный ответ на сложный вопрос. Кстати, у вас будет возможность померяться «силами» оналайн с другими игроками. Соревнуются игроки за позиции в рейтинге, формирующегося по сумме очков, полученных в ходе всех раундов.

Ответы к игре 100 к 1

Если вы хотите победить и знать сто к одному ответы на все вопросы, у вас есть несколько вариантов. Первый путь самый сложный: вам придется долго играть и упорно запоминать все ответа. Вот когда вы сможете ответить на все 100 к 1 почему и 100 к 1 где, только тогда у вас получится занять свое место в пантеоне лидеров приложения. Второй вариант попроще, можно заплатить, обменять эти деньги на голоса и на очки, чтобы купить подсказки. Максимум подсказок пять – а значит победа будет у вас в кармане. Самый легкий способ, который предлагает вам stevsky.ru, найти все подсказки на нашем сайте. Играйте в свое удовольствие, ведь теперь вам не нужно искать 100 к 1 где ответы

Сто к одному ответы

После подключения к приложению обоих соперников, игровой процесс сто к одному можно разделить на три раунда, каждый из которых получает уникальный вопрос. Стоит отметить, что эти вопросы собираются среди самих игроков и не являются сгенерированными. Введенные варианты проверяются с использованием синонимов и по правилам русского языка.
На первом этапе вам предлагается одинарная игра, когда соперники должны по очереди называть свой ответ на заданный вопрос. В случае угадывания одного из шести популярных ответов, позиция открывается и очки попадают в общую копилку. В противном случае, игроку засчитывается ошибка в

100 к 1. Что бывает когда ошибок больше? Как только более слабый соперник стратит трижды, все очки из копилки получит его конкурент.
На втором этапе вы сможете сыграть в так называемую Двойную игру. Правила здесь аналогичны, однако очков начисляется в два раза больше.
Ну и игра Наоборот. В этой игре у каждого соперника есть только одна попытка. Нужно написать наименее популярный ответ на заданный вопрос, который, несмотря на это, имеется в списке 6 наиболее популярных. Если не сделаете ошибки и найдете нужный ответ – копилка будет ваша! Удачной игры!

100 к 1 ответы на вопросы 1-100
100 к 1 ответы на вопросы 101-200
100 к 1 ответы на вопросы 201-300

Теги: 100 к 1, 100 к 1 ответы, 100 к 1 почему, 100 к 1 где, 100 к 1 где ответы, игра 100 к 1, играть в 100 к 1, ответы к игре 100 к 1, вопросы к игре 100 к 1, 100 к 1 что бывает, ответы к игре 100 к 1, сто к одному ответы, игра сто к одному, сто к одному

< Предыдущая		Следующая >

---

Новые материалы по этой тематике:

• 03/06/2014 — Найди кота ответы ВКонтакте все уровни
• 31/05/2014 — Wormix (Вормикс) – читы, коды, прохождение
• 30/05/2014 — Drakensang Online – прохождение, секреты
• 30/05/2014 — Music Wars вконтакте — читы, коды, секреты, скачать на андроид
• 18/12/2013 — ВКонтакте планирует издавать игры для ОС iOS и Android
• 11/12/2013 — Брендомания ответы уровень 1
• 06/12/2013 — Копатель онлайн — читы на игру

Старые материалы по этой тематике:

• 24/11/2013 — Найди кота — ответы в Контакте
• 04/11/2013 — Алхимия Шарарам — ответы

---

BIZZARO — Умные часы CIW101BT

• Обзор
• Технические характеристики
• Комплектация
• Драйверы и ПО
• 3D-Фото

С помощью умных часов BIZZARO CiW101BT можно не только следить за временем, но ещё быть в курсе всех событий, не обращаясь постоянно к экрану смартфона. Соединение по Bluetooth позволят умным часам взять на себя часть важных функций и предоставить всю входящую информацию. На экране часов отобразятся сообщения, пришедшие по электронной почте, SMS, из социальных сетей, различных мессенджеров и Skype. Получение сопровождается лёгкой вибрацией или звуковым сигналом. Предусмотрена возможность ответа на любое сообщение или отправка нового. Благодаря режиму hands-free, встроенному динамику и микрофону можно даже вести беседу, не вынимая смартфон из сумки или кармана. Контакты автоматически синхронизируются, и вы имеете полноценную адресную книгу в часах. BIZZARO CiW101BT способны работать с любыми смартфонами на базе Android или iOS.

 

Часы оборудованы цветным ёмкостным дисплеем, размером 1.54″ и разрешением 240х240 pixels, на котором очень удобно просматривать сообщения и писать ответы. Присутствуют и стандартные, на сегодняшний день, функции органайзера: будильник, калькулятор и календарь. Полезная программа «Шагомер» поможет следящим за своим здоровьем мониторить двигательную активность в течение дня и подсчитает затраченные калории. Любители спорта особенно оценят эти возможности.

 

Умные часы умеют удалённо управлять аудиоплеером — переключать треки, регулировать громкость, ставить на паузу и возобновлять воспроизведение. Также есть возможность управлять и камерой телефона, используя экран часов как видоискатель — очень полезная функция при групповой съёмке с вашим участием. Подключив hands-free гарнитуру можно прослушивать FM-радио. Функция «Вы забыли смартфон» проинформирует о том, что расстояние между вами и телефоном превысило радиус действия Bluetooth и позволит не потерять аппарат.

 

Умные часы удобно сидят на руке. Управление интуитивно, к нему можно легко привыкнуть. Внешний вид экрана меняется совершенно не сложно. Проведя пальцем по дисплею можно с легкостью поменять изображение циферблата, выбрав понравившееся из трёх предустановленных. Длительность работы от Lithium-Polymer аккумулятора объёмом 450 mAh составляет до 3‑х часов в режиме разговора и 100 часов в режиме ожидания. Умные часы BIZZARO CiW101BT станут необходимым дополнением для всех владельцев смартфонов.

        

 

Купить

 

Экран	Размер	1.54″
	Разрешение	240 × 240 pixels
	Тач-скрин	Ёмкостной
Система	ОС	MTK OS
	Язык	Мультиязычная
Порты ввода-вывода	Внутренний	Память 128MB+64MB
	USB	micro USBx1
	Bluetooth	3,0
	Звук	Вибрация, проиграватель MP3
Встроенные приложения	Шагомер	Измерение количества шагов, подсчёт калорий
	Калькулятор, Календарь, Будильник
Обмен данными со смартфоном	Контакты	Синхронизация контактов Андроид/iPhone, 500 контактов
	Отображение номера звонящего	Отображается номер телефона или Имя звонящего (после выполнения синхронизации контактов)
	SMS	После установки приложения на смартфон (Android) доступно уведомление о входящих SMS, отображение текста SMS.
	Входящие звонки	Ответ на входящие звонки по громкой связи или через Bluetooth наушник (Android/iPhone). Ответ на SMS, написание новой SMS
	Исходящие звонки	Набор номера из списка контактов или ввод с клавиатуры (Android/iPhone)
	Забыл телефон	Звуковое предупреждение при выходе из зоны действия Bluetooth телефона
	Мультимедиа	Проигрывание файлов MP3, MP4, 3gp, avi с телефона
		Связь с камерой телефона
		FM-радио
		Запись голоса
	Прочие оповещения	Оповещение о событиях Facebook, Twitter, Skype (Android)
Аккумулятор	Ёмкость	450mAh
	Материал	Lithium-Polymer
	Время ожидания	100 часов
	Время разговора	До 3-х часов
	Проигрывание музыки	До 7 часов
Механические характеристики	Цвет	Чёрный, синий
	Материал	Корпус – пластик; ремень – силикон
	Вес	65 г.
	Размер	38.7 × 41 × 13 мм
Комплектация	Переходник для наушников, USB — кабель; Руководство пользователя; Гарантийный талон

        

 

Купить

 

 

• Переходник для наушников
• USB — кабель
• Руководство пользователя
• Гарантийный талон

Купить

 

 

Программа синхронизации для CIW101BT

 

 

 

Купить

 

Время, когда все «исправили» самую умную женщину в мире

Закари Крокетт

По общему мнению, Мэрилин вос Савант была вундеркиндом.

Молодой ученый родился в Сент-Луисе, штат Миссури, в 1946 году. Он быстро развил способности к математике и естественным наукам.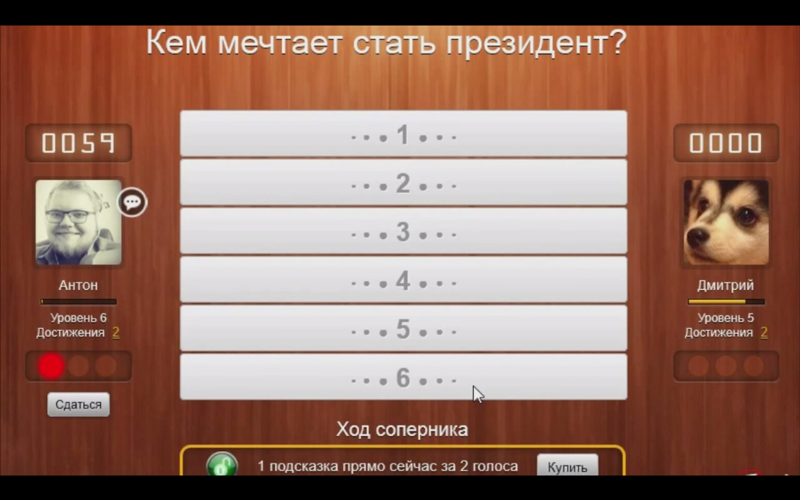 В возрасте 10 лет ей дали два теста интеллекта — Стэнфорд-Бине и Мега-тест, — оба из которых показали ее умственные способности на уровне 23-летнего. Она попала в список Книга рекордов Гиннеса за «самый высокий IQ в мире» и, как следствие, получила международную известность.

Несмотря на свой статус «самой умной женщины в мире», вос Савант утверждала, что попытки измерить интеллект «бесполезны», и отвергала тесты IQ как ненадежные. В середине 1980-х, имея полную свободу выбора карьеры, она собрала чемоданы и переехала в Нью-Йорк, чтобы стать писателем.

Здесь она поймала прорыв: когда журнал Parade Magazine написал о ней профиль, читатели ответили таким количеством писем, что издание предложило ей постоянную работу. Вскоре после этого она основала известную теперь еженедельную колонку «Спросите Мэрилин», в которой она отвечала (и продолжает отвечать по сей день) на различные академические вопросы и логические головоломки. Именно в теле одной из этих колонок вос Савант разжег одну из самых жарких статистических битв 21 века.

Когда вос Савант вежливо ответила на вопрос читателя о проблеме Монти Холла, тогдашней относительно неизвестной вероятностной головоломке, она и представить себе не могла, что развернется: хотя ее ответ был правильным, она получила более 10 000 писем, многие из отметили ученые и доктора наук, сообщив ей, что она безмозглая идиотка.

То, что последовало за вос Савант, было кошмарным путешествием, изобилующим обзывательствами, гендерными предположениями и академическими преследованиями.

Проблема Монти Холла: Краткая история

Представьте, что вы участвуете в телевизионном игровом шоу, и ведущий представляет вам три закрытые двери. За одним из них стоит сверкающий новенький Lincoln Continental; за двумя другими — вонючие старые козы. Хозяин умоляет вас выбрать дверь, и вы выбираете дверь №1. Затем ведущий, хорошо осведомленный о том, что происходит за кулисами, открывает дверь №3, показывая одну из коз.

«Теперь, — говорит он, поворачиваясь к вам, — вы хотите оставить дверь №1 или переключиться на дверь №2?»

По статистике, какой выбор дает вам автомобиль: оставить прежнюю дверь или поменять? Если вы, как и большинство людей, утверждаете, что ваши шансы 50 на 50, вы ошибаетесь — если, конечно, вы любите коз так же сильно, как и новые машины, и в этом случае вы выиграете в 100% случаев.

Вольно основанный на известном телевизионном игровом шоу Давайте заключим сделку , представленный выше сценарий, более известный как «Проблема Монти Холла», представляет собой довольно известный вероятностный вопрос. Несмотря на его обманчивую простоту, некоторые из самых ярких умов мира — профессора Массачусетского технологического института, известные математики и стипендиаты MacArthur «Genius» — с трудом могли понять ответ. На протяжении десятилетий она вызывала бурные дебаты в классах и лекционных залах.

Исторически так сложилось, что задаче Монти Холла предшествовало несколько очень похожих головоломок.

В парадоксе коробки Жозефа Бертрана (1889 г.) представлены три коробки: одна с двумя золотыми монетами, другая с двумя серебряными монетами и последняя с одной каждой из них. Предполагая, что участник достает из коробки одну золотую монету, задача затем спрашивает, какова вероятность того, что другая монета в этой коробке золотая. Бертрана, который пришел к выводу, что вероятность равна ⅔, хвалили за его способность смотреть за пределы очевидного.

Вторая итерация этого парадокса, Задача трех заключенных (1959), представляет собой статистически идентичный сценарий с тем же исходом. «[Это] удивительно запутанная маленькая проблема», — самодовольно писал позже ее создатель, обозреватель журнала Scientific American Мартин Гарднер. «Ни в какой другой области математики эксперты не ошибаются так легко, как в теории вероятностей».

Проблема Монти Холла, впервые представленная в письме редактору The American Statistician в 1975 году, также была нелогичной. В этом письме Стив Селвин, профессор Калифорнийского университета в Беркли, изложил ситуацию во вступлении к этой статье и заявил, что смена дверей дает ⅔ шанса на выигрыш автомобиля, в то время как сохранение исходной двери приводит к выигрышу только ⅓ времени.

В течение следующего десятилетия или около того проблема Монти Холла несколько раз появлялась, сначала в головоломке Journal of Economics Perspectives Барри Нейлбаффа, а затем в выпуске Bridge Today Филипа Мартина за 1989 год. Ни одна из логик не была опровергнута, и проблема привлекла относительно мало внимания.

Затем, после 15 лет без происшествий, проблема Монти Холла была воскрешена Мэрилин вос Савант — и последовала настоящая буря дерьма.

Фиаско Мэрилин вос Савант

В сентябре 1990 года Мэрилин вос Савант посвятила одну из своих колонок вопросу читателя, который представил вариант задачи Монти Холла:

«Предположим, вы участвуете в игровом шоу и вам предоставляется выбор из трех дверей. За одной дверью машина, за другими козы. Вы выбираете дверь, скажем, №1, и хозяин, который знает, что находится за дверью, открывает другую дверь, скажем, №3, в которой есть коза. Он говорит вам: «Вы хотите открыть дверь № 2?» В ваших интересах ли поменять дверь?

«Да; тебе следует переключиться, — ответила она. «Первая дверь имеет шанс выиграть 1/3, а вторая дверь имеет шанс 2/3».

Хотя ее ответ был верным, многие ученые отреагировали на него с возмущением. В последующие месяцы вос Савант получила более 10 000 писем, в том числе пару писем от заместителя директора Центра оборонной информации и специалиста по математической статистике из Национального института здравоохранения, во всех из которых утверждалось, что она совершенно некомпетентна:0005

Ты все испортил, и ты все испортил! Поскольку вам, кажется, трудно уловить основной принцип работы, я объясню. После того, как ведущий показывает козла, у вас теперь есть шанс один к двум быть правым. Независимо от того, измените ли вы свой выбор или нет, шансы одинаковы. В этой стране достаточно математической неграмотности, и нам не нужно, чтобы самый высокий в мире IQ распространялся дальше. Стыд!
Скотт Смит, доктор философии.
Университет Флориды

Могу ли я предложить вам получить и обратиться к стандартному учебнику по вероятности, прежде чем вы снова попытаетесь ответить на вопрос такого типа?
Чарльз Рид, доктор философии.
Университет Флориды

Я уверен, что вы получите много писем на эту тему от старшеклассников и студентов колледжей. Возможно, вам следует сохранить несколько адресов для помощи в будущих колонках.
У. Роберт Смит, доктор философии.
Университет штата Джорджия

Вы совершенно неправы в вопросе об игровом шоу, и я надеюсь, что это противоречие привлечет внимание общественности к серьезному национальному кризису в математическом образовании. Если вы сможете признать свою ошибку, вы внесете конструктивный вклад в решение прискорбной ситуации. Сколько нужно разгневанных математиков, чтобы заставить вас передумать?
Э. Рэй Бобо, доктор философии.
Джорджтаунский университет

Вы совершили ошибку, но посмотрите на нее с положительной стороны. Если бы все эти доктора наук были неправы, у страны были бы очень серьезные проблемы.
Эверетт Харман, доктор философии.
Научно-исследовательский институт армии США

Ты коза!
Гленн Калкинс
Западный государственный колледж

Возможно, женщины смотрят на математические задачи иначе, чем мужчины.
Дон Эдвардс
Санривер, Орегон

Возмущение было настолько огромным, что вос Савант была вынуждена посвятить три последующих колонки объяснению, почему ее логика была верна. Даже после ее четко сформулированных и четких ответов ее продолжали ругать. «Я все еще думаю, что вы ошибаетесь», — написал один человек почти год спустя. «Есть такая вещь, как женская логика».

Тем не менее, цифры, стоящие за выводом вос Саванта, не лгут.

Разоблачение проблемы Монти Холла

Поскольку две двери (одна с машиной, а другая с козой) остаются после того, как ведущий открывает дверь №3, большинство предположило бы, что вероятность выбора машины равна ½. Это не вариант.

«Шансы на выигрыш 1/3 при первом выборе не могут возрасти до 1/2 только потому, что организатор открывает дверь для проигрыша», — пишет Вос Савант. Действительно, если вы наметите шесть игр, исследуя все возможные исходы, станет ясно, что смена дверей приводит к выигрышу в 9 играх.0027 две трети (66,6%) времени , и сохранение исходной двери приводит к выигрышу только одна треть (33,3%) времени:

Еще один способ взглянуть на это — сломать отключите все возможности переключения дверей. Как показано ниже, 6 из 9 возможных сценариев (две трети) приводят к выигрышу автомобиля:0014 Увеличивает ли смена дверей наши шансы на победу?

Краткий ответ заключается в том, что ваши начальные шансы на победу с дверью №1 (⅓) не меняются просто потому, что ведущий показывает козу за дверью №3; вместо этого действие Холла увеличивает вероятность того, что вы выиграете, переключившись на ⅔.

Вот еще один способ визуализировать это. Представьте, что вместо трех дверей Монти Холл представляет вам 100 дверей; за 99 из них козы, а за одним из них машина. Вы выбираете дверь №1, и ваши первоначальные шансы выиграть машину теперь составляют 1/100:9.0005

Тогда давайте предположим, что Монти Холл открывает 98 других дверей, показывая козла за каждой. Теперь у вас есть два варианта: оставить дверь №1 или переключиться на дверь №100:

Когда вы выбираете дверь №1, вероятность того, что машина находится за одной из других дверей, составляет 99/100. Тот факт, что Монти Холл показывает 98 коз, не меняет этих первоначальных шансов — он просто «сдвигает» этот шанс 99/100 на дверь № 100. Вы можете либо придерживаться своего первоначального выбора с коэффициентом 1/100, либо переключиться на дверь № 100, с гораздо более высокой вероятностью выиграть машину.

Тем не менее, в то время как математика и цифры подтверждают утверждение вос Савант о том, что шансы на победу увеличиваются до ⅔, когда вы меняете дверь, необходимо учитывать другие факторы, которые она не затрагивает в своем ответе.

Психология рационализации

Монти Холл, ведущий программы «Давай заключим сделку»

В 1992 году, когда назревал спор по поводу ответа Воса Саванта, Монти Холл — ведущий игрового шоу и тезка проблемы — взял интервью у Нью-Йорк Таймс .

Холл пояснил, что все работало немного иначе, чем сценарий, представленный читателем Parade в колонке Воса Саванта. В реальном шоу, например, он сохранил за собой право предлагать участникам деньги НЕ переключаться. Подобные детали, по его словам, изменили мышление участника:

«[После того, как я открыл дверь с помощью козла], они думали, что шансы на их дверь теперь выросли до 1 к 2, поэтому они ненавидели отказываться от двери, независимо от того, сколько денег я предлагал… Чем выше Я получил, тем больше [они] думали, что машина была за [другой дверью]. Я хотел убедить [их] переключиться туда. Это то, что я могу делать, когда контролирую игру. Вы можете подумать, что у вас есть вероятность, когда вы будете следовать ответу в ее колонке, но есть психологический фактор, который следует учитывать».

«Психологический фактор», о котором упоминает Холл, переносится из правил шоу в разновидность задачи, которую мы представили в этой статье. Как у участников, так и у тех, кто решает проблемы, проблема Монти Холла вызывает когнитивный диссонанс — термин, который психологи используют для описания «психического стресса, испытываемого человеком, который одновременно придерживается двух или более противоречивых убеждений, идей или ценностей или сталкивается с новой информацией, которая противоречит существующим убеждениям, идеям или ценностям».

Когда люди сталкиваются с доказательствами, которые «несовместимы с их убеждениями» (т. е. шансы на победу при смене дверей составляют ⅔ вместо ½), они сначала реагируют, опровергая информацию, а затем объединяются с единомышленниками-несогласными и отстаивать свое упрямое мнение. Именно таков менталитет тысяч скептиков вос Саванта.

***

Спустя более 25 лет споры о семантике проблемы Монти Холла и ответе Вос Саванта все еще широко распространены — в основном вокруг хитросплетений действий хозяина.

«Наш мозг просто не приспособлен для решения вероятностных задач, поэтому я не удивлен, что были ошибки», — сказал репортеру профессор статистики из Стэнфорда Перси Диаконис несколько лет назад. «[Но] строгим аргументом будет то, что на вопрос нельзя ответить, не зная мотивации хозяина».

В конце концов, многие из тех, кто написал, чтобы исправить математику воса Саванта, отступили и признали, что они были ошибкой.

Упражнение, предложенное вос Савант для лучшего понимания проблемы, вскоре было внедрено в тысячи классных комнат по всей стране. Были построены компьютерные модели, подтверждающие ее логику, и постепенно восстановилась поддержка ее интеллекта. В то время как ранее только 8% читателей верили в ее логику, к концу 19 века это число возросло до 56%.92 года, пишет вос Савант; среди ученых первоначальная поддержка с 35% выросла до 71%.

Среди новообращенных был Роберт Сакс, профессор математики из Университета Джорджа Мейсона, который сначала написал вос Савант неприятное письмо, в котором сказал ей, что она «облажалась», и предложил помочь «объяснить». Поняв, что на самом деле он был не прав, он почувствовал себя обязанным послать ей еще одно письмо — на этот раз с раскаянием в своей самоуверенности.

«После того, как я вынул ногу изо рта, я теперь ем скромный пирог», — написал он. «Я поклялся в качестве покаяния ответить всем людям, которые писали, чтобы осудить меня. Это было сильное профессиональное смущение».

Прайсономика написала две книги. Один для скептиков, другой оптимистов. Выбери свое приключение  → Все фигня или  900s Бизнес-модель 900s

0027 Подпишитесь на нашу рассылку . Этот пост был первоначально опубликован 19 февраля 2015 года. Опубликовано 2 августа 2016 г. Закари Крокеттом

---

13 самых умных людей в истории мира

Мы знаем, что эти люди исключительно умны и талантливы. Но насколько они умны по сравнению друг с другом? Вот 13 самых умных гениев в мире, или, по крайней мере, то, что нам предоставили два западных научных исследования.

Как мы получаем IQ

Оценить уровни IQ людей, которые умерли за столетия до того, как был разработан точный научный бенчмаркинг интеллекта, сложно; но здесь у нас есть два наиболее часто цитируемых исследования: «Ранние умственные черты 300 гениев» 1926 года американского психолога Кэтрин Кокс, которая вычислила IQ гениев с пятнадцатого по девятнадцатый век; и Книга гениев 1994 года Тони Бьюзена, эксперта по обучению английскому языку, который составил более широкий список 100 величайших гениев нашего мира.

Несоответствие в их списках очевидно. У Бьюзена на первом месте был Да Винчи с IQ 220, а Кокс поставил художнику-изобретателю всего 180 баллов. Тем не менее, забавно усреднять два списка, чтобы увидеть, кто из этих гениев превосходит своих собратьев-мозговиков в чистом показателе IQ. Те, кто не попал в первую двадцатку обоих списков, автоматически выбывают из игры, но это не значит, что они менее умны, чем люди из этого списка (мы никогда не сможем сказать наверняка).

Более того, в список не вошли такие гении двадцатого века, как Альберт Эйнштейн, Энрико Ферми и Стивен Хокинг. Точно так же вы заметите, что это европейские гении; следовательно, мастера разума из Азии тоже не появлялись. Эти вещи в стороне и без дальнейших церемоний, вот они: самые гениальные из гениев и их умопомрачительные уровни IQ и достижения.

13. Чарльз Диккенс – 

Уровень IQ: 165

Английский писатель, поэт, общественный критик. Он известен своими литературными шедеврами, среди которых «Большие надежды», «Оливер Твист», «Рождественская история» и «Дэвид Копперфильд». Он также считается величайшим писателем викторианского периода, когда Англия безраздельно властвовала в литературном, научном, торговом и военном мире.

12. Рафаэль – 

Уровень IQ: 170

Еще один художник эпохи Возрождения попал в наш список, итальянский современник да Винчи и Микеланджело. Рафаэль был художником и архитектором, третьим членом тройки великих мастеров Высокого Возрождения. Его самые известные работы включают «Распятие Монда», «Изложение Христа» и «Преображение».

11. Майкл Фарадей —

Уровень IQ: 175

Английский ученый, получивший небольшое формальное образование. Его работы продвинули области электромагнетизма и электрохимии, предшественников высоких технологий, которыми мы пользуемся сегодня. Свидетельством его гениальности являются многочисленные научные принципы, названные в его честь: закон индукции Фарадея; Эффект Фарадея: клетка Фарадея; парадокс Фарадея; колесо Фарадея; и волна Фарадея среди других. Его исследования сделали возможными более поздние изобретения в области электричества и тока.

10. Барух Спиноза – 

Уровень IQ: 175

Голландский философ. Он был одним из первых, кто заложил основу эпохи Просвещения, когда наука бросила вызов статус-кво церкви. Эпоха привела к большим скачкам в области науки, политики и экономики, во главе которых, среди прочего, стоял великий труд Спинозы «Этика», который ставит под сомнение подлинность еврейской Библии.

9. Микеланджело – 

Уровень IQ: 177

С французским философом связан еще один представитель итальянского Возрождения, скульптор, художник, архитектор, поэт и инженер Микеланджело. Известен своими шедеврами, а именно «Давид», «Пьета», «Сикстинская капелла», «Страшный суд» и «Сотворение Адама». Многие эксперты даже утверждали, что он величайший художник всех времен, субъективная оценка, но не лишенная оснований, учитывая его вклад в искусство Высокого Возрождения.

8. Дезидериус Эразм – 

Уровень IQ: 177

Голландский гуманист, теолог, социальный критик. Он был активным сторонником религиозной терпимости в эпоху Реформации, когда католики и протестанты вцепились друг другу в горло. Используя гуманистические приемы, он подготовил новую партию латинских и греческих изданий Нового Завета, которые стали влиятельными материалами в это неспокойное время. Несмотря на критику церкви, Эразм сохранил свою католическую веру, полагая, что католическая иерархия может быть реформирована внутри без необходимости создания ответвления веры.

7. Рене Декарт – 

Уровень IQ: 177

Французский философ, математик и писатель. Его называют отцом современной философии из-за его сочинений. Примечательно, что «Размышления о первой философии» до сих пор являются стандартным справочником в университетах по всему миру. Он также известен своим математическим вкладом, в частности, декартовой системой координат, а также тем, что он объединил алгебру и геометрию, что сделало возможным развитие исчисления.

6. Галилео Галилей – 

Уровень IQ: 182

Итальянский физик, астроном, математик, философ. Он наиболее известен тем, что подарил нам телескоп. Но это лишь малая толика в его широкомасштабных научных достижениях, а именно открытие планетарных объектов, таких как Каллисто, галилеевых спутников, Европы, Ганимеда и Ио. Он также отвечал за подтверждение посредством фактических наблюдений гелиоцентрической природы Солнечной системы — Солнце находится в центре, а планеты вращаются вокруг него — что в свое время поставило его под прицел Инквизиции.

5. Джон Стюарт Милль —

Уровень IQ: 182,5

Английский философ и политический экономист. Он наиболее известен своим влиятельным вкладом в либерализм, идею индивидуальной свободы в отличие от неограниченного государственного контроля над экономикой. Метод Милля также широко используется сегодня, чтобы прийти к выводу с помощью индукции, инструмента, который юристы и ученые использовали для продвижения своих аргументов.

4. Готфрид Вильгельм Лейбниц –

Уровень IQ: 191

Немецкий философ и математик. Считается, что он внес свой вклад в развитие исчисления, независимого от Ньютона, особенно в его работах «Закон непрерывности» и «Трансцендентальный закон однородности». Он также был плодовитым изобретателем в области механических калькуляторов, позволяющих таким негениальным людям, как мы, решать сложные математические задачи с помощью этого устройства.

3. Исаак Ньютон –

Уровень IQ: 192

Английский физик и математик. Считается, что он разработал большую часть исчисления, строительных блоков сегодняшних инженерных подвигов. Его «Математические принципы натуральной философии» — одна из самых влиятельных научных работ, знаменующих эпоху просвещения, когда Европа вступила в эпоху достижений, породивших современные технологии.

2. Леонардо да Винчи – 

Уровень IQ: 200

Человек итальянского Возрождения. Его гений распространялся на науку и искусство. Да Винчи, наиболее известный своей Моной Лизой, на самом деле был больше, чем исключительно талантливым художником. Он был математиком, инженером, изобретателем, скульптором, архитектором, геологом, картографом, ботаником и писателем. Он был воплощением человека эпохи Возрождения, неся в мир свое богатство знаний, чтобы изменить судьбу человечества.

1. Иоганн Вольфганг фон Гёте – 

Уровень IQ: 220

Немецкий поэт, прозаик, драматург, политик и дипломат. Он наиболее известен своими литературными произведениями, такими как «Страдания юного Вертера», «Буря и натиск» и «Фауст». Хотя его лучше всего считают литературным гением, Гёте также занимался научными исследованиями, особенно в области естествознания. У него была обширная коллекция минералов в рамках его обширных исследований в области геологии.

Эти люди могут показаться замечательными и редкими, но гений встречается чаще, чем мы думаем.