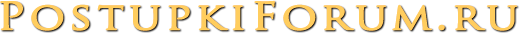Психогеометрический тест, который работодатели предлагают пройти на собеседовании / AdMe
В 1978 году специалист по социально-психологической подготовке Сьюзан Деллингер представила миру свой психогеометрический тест. Сегодня многие работодатели предлагают пройти его на собеседовании: он указывает на сильные и слабые стороны человека с большой точностью.
ADME предупреждает: если вам предложат пройти этот тест, будьте уверены — одобрение вашей кандидатуры будет зависеть от его результата, а не от хорошего резюме.
Взгляните на эти геометрические фигуры
Какая из данных фигур вам ближе? Выберите ту, которую ассоциируете с собой, и приступайте к изучению результатов
1. Квадрат
Трудолюбие, потребность доводить дело до конца, упорство — основные качества Квадратов. Терпение и выносливость делают их лучшими специалистами в своей области. Этому также способствует сильная потребность в получении новой информации.
Знания Квадратов систематизированы и разложены по полочкам.
Они не склонны к догадкам, а полагаются только на свои вычисления и очень внимательны к деталям. Предсказуемая жизнь — это их идеал. Им не по душе, когда меняется привычный ход событий.
Пристрастие к деталям лишает Квадратов оперативности. Аккуратность и приверженность к соблюдению правил могут развиться до крайности. Помимо прочего, их рациональность и эмоциональная сухость мешают быстро наладить контакт с окружающими.
2. Треугольник
Треугольник — энергичная и сильная личность. Их характерная особенность — умение концентрироваться на главном. Они способны глубоко и быстро анализировать ситуацию и сосредотачиваются на сути, не придавая большого значения деталям.
Это очень уверенные в себе люди, которые хотят быть во всем правыми. Из-за потребности управлять текущим положением дел и решать за других Треугольник становится личностью, которая постоянно соперничает и конкурирует с другими. Они часто бывают категоричны, не переносят возражений и с трудом признают свои ошибки.
Для них очень важна карьера, и они стремятся к высокому статусу. Их главное отрицательное качество — направленность на себя, сильный эгоцентризм.
3. Зигзаг
Зигзаг — творческая личность. Таким людям свойственны интуитивность и образность мышления. Последовательность — это не их стиль. Мысли Зигзага совершают отчаянные прыжки. Они не зацикливаются на деталях, тем самым упрощая картину мира. Это позволяет им создавать гармоничные образы и во всем видеть красоту. У таких людей сильно развито эстетическое чувство.
Зигзаги не могут трудиться там, где есть строгие обязанности. В работе для них важна независимость. Когда Зигзаг находится там, где ему комфортно, он начинает работать, выполняя свое основное назначение — генерирование новых методов работы и идей.
Такие люди — идеалисты. Из-за этого им свойственны наивность и непрактичность. Из всех 5 фигур Зигзаг самый легковозбудимый. Они несдержанны, что часто мешает им воплощать свои идеи в жизнь.
4.
КругПрежде всего Круг заинтересован в хороших межличностных отношениях. Эти люди очень доброжелательны. Круг способен сплотить коллектив и создать крепкую семью. Им свойственны повышенная чувствительность и сильная эмпатия. Они хорошо «читают» людей и могут быстро распознать обманщика или притворщика.
Такие люди направлены на других людей, а не на дело. Чтобы сохранить мир, они могут отказаться от собственной позиции, потому что самое тяжелое для Круга — вступать в конфликт. Решительность таким людям чужда, и они часто не могут подать себя так, как хотелось бы.
В вопросах морали и справедливости Круги проявляют завидную твердость. Их мышление заточено на чувства и моральные ценности. Они стремятся найти нечто общее в различных точках зрения.
5. Прямоугольник
Прямоугольник — это временная форма личности. Это люди, которые недовольны своим нынешним образом жизни и находятся в поисках лучшего положения.
Характерная черта таких людей — непредсказуемость поступков во время переходного периода.
Как правило, у них низкая самооценка, и они ищут что-то новое в стремлении стать лучше: это касается работы, имиджа и так далее.
Прямоугольникам свойственны пытливость, искренний интерес к происходящему и смелость. Они открыты для новых идей и с легкостью усваивают все новое. С другой стороны, в переходный период они становятся легкой добычей для манипуляторов, поскольку их состоянию свойственны внушаемость и доверчивость.
Узнали ли вы себя в описании выбранной фигуры?
AdMe/Наука/Психогеометрический тест, который работодатели предлагают пройти на собеседовании
Как быстро оценить кандидата: популярные психологические тесты для собеседований
Психологические тесты проводят на собеседованиях практически в каждой компании. DISC, STAR и другие тестирования, на которых оцениваются необходимые навыки кандидата — достаточно эффективны. Но что, если у рекрутера недостаточно времени на интервью или не было возможности как следует подготовиться? В этом случае вам помогут быстрые психологические тесты, которые определят, на какую должность подойдет кандидат.
Психогеометрический тест
Чтобы определить особенности поведения и индивидуальные черты характера, используйте психогеометрический тест. За 2-3 минуты вы сможете определить необходимую компетенцию для кандидата на любую должность.
Как провести? При проведении этого теста, рекрутер предлагает соискателю расположить такие геометрические фигуры, как квадрат, прямоугольник, треугольник, круг и зигзаг в произвольном порядке. Первой располагается самая значимая для кандидата фигура, последней — наименее привлекательная.
Интерпретация результатов. Фигуры, которые предпочитает кандидат, отражают его ярко выраженные черты характера.
| Фигуры | Качества |
| Квадрат | Пунктуальный, организованный, соблюдает правила. Должности: секретарь, бухгалтер, инженер. |
| Треугольник | Стремится к власти, трудолюбивый, решительный, уверенный в себе. Должности: лидерские позиции, руководители, топ-менеджеры |
| Круг | Уравновешенный, ориентирован на других, имеет высокие коммуникативные навыки, эмпатичный. Должности: психолог, менеджер по работе с клиентами, HR-менеджер. |
| Прямоугольник | Позитивный, инициативный, временами неопределенный, неконфликтный, коммуникабельный. Должности: менеджер по продажам, менеджер по работе с клиентами. |
| Зигзаг | Креативно мыслит, постоянно обучается, любит перемены, владеет развитой интуицией. Должности: дизайнер, художник, креативщик. |
Плюсы теста: не требует подготовки у рекрутера и не занимает много времени у кандидата. Поскольку психогеометрический тест весьма распространен, кандидат может знать, как интерпретируются результаты, но с другой стороны он не может предугадать, какой психотип вы ищете.
Недостатки: этот тест не отражает полную картину компетенций и не полностью раскрывает психотип кандидата.
Тем более, на его результаты может влиять множество факторов. Поэтому, данный тест рекомендовано использовать в сочетании с другими.
Тест «Любимый цвет»
Этот тест отлично подойдет для оценки черт характера кандидата и определить те, которые необходимы для конкретной должности. Например, если вы в поиске менеджера по продажам, то эффективнее всего будет работать тот соискатель, который предпочитает красные и желтые цвета.
Как провести? Вам необходимо подготовить 8 карточек с цветами: синий, зеленый, красный, желтый, фиолетовый, коричневый, серый, черный. Кандидат должен расположить все цвета в ниспадающем порядке от самого приятного до самого неприятного.
Интерпретация результатов. Давайте разберем, что означают эти цвета и их порядок.
Cиний. Потребность в эмоциональном спокойствии, внутренней гармонии, отдыхе. Такие личности стремятся к упорядоченности и стабильности, они действуют по установленному порядку.
Любители синего спокойны, склонны доверять людям и следуют морально-этическим принципам.
Те, кто ставят синий на 6,7 и 8 позиции, отличаются беспокойным поведением и длительным внутренним напряжением. Они мечтают избавиться от обременительных обязательств.
Зеленый. Любители зеленого стремятся к улучшению условий жизни, отличаются хорошей логикой и критическим анализом, а также стремятся к признанию. Они контролируют не только свою жизнь, но и жизнь окружающих, стараясь оставаться эффективными и нужными.
Противники зеленого страдают от нехватки признания и испытывают трудности в борьбе с препятствиями к заветной цели. Чем дальше стоит зеленый в списке цветов, тем больше кандидат испытывает желание самоутвердиться, имеет склонность к критике и проявляет упрямство.
Красный. Этот цвет любят волевые и активные. Они знают чего хотят, живут настоящим и практически всегда добиваются своих целей. «Красные» успешно работают как в коллективе, так и самостоятельно.
Отвергают этот цвет те, кому не хватает жизненной энергии. На последние места также красный ставят те, кто видит в нем угрозу. Они защищаются от всего, что может выйти из под контроля и осложнить ситуацию.
Желтый. Те, кто предпочитает желтый цвет, всегда идут вперед. Они — амбициозны, оптимистичны и заряжают других энергией. Также, как и «зеленые», стремятся занять высокое положение, но делают это более расслабленно и сдержанно.
Желтый цвет не любят люди, которые переживают в своей жизни не самый легкий период или по натуре являются одиночками. Бывает так, что отвергая желтый, человек ставит на первое место синий. Это может означать желание мира и спокойствия и тенденцию держаться за привычное, не принимая изменений.
Фиолетовый. Любителей фиолетового едва ли можно назвать реалистами. Они любят очаровывать других, вызывать восторг и восхищение. «Фиолетовых» необходимо постоянно хвалить и быть готовым к их эмоциональной неустойчивости.
Они остро реагируют на критику и предпочитают не брать на себя ответственность.
Противники фиолетового сдержаны в эмоциях и критичны. Им трудно заводить действительно близкие и прочные отношения с другими людьми.
Коричневый. Те, кто ставят коричневый на первое и второе места, ценят семейный уют и безопасность. Они обладают ярко выраженным «стадным чувством» и нуждаются в физическом ощущении благополучия.
Если коричневый располагается с 5 по 7 место, то это не имеет особого значения в оценке кандидатов. Но если он занимает 8 место — перед вами типичный индивидуалист.
Серый. Этот цвет еще называют бесцветным. Он нейтрален, как и поведение «серых». Если он стоит на первом месте, это означает, что человек стремится отделиться от остального мира, быть незаметным. Он контролирует свои действия, и как-бы стремится улучшить обстоятельства своим бездействием.
Те, кто ставят серый на последнее место могут быть излишне назойливыми и любопытными.
Они считают этот цвет скучным, предпочитая другие цвета с конкретными стимулами и используют любую возможность в достижении своих целей.
Черный. По своей природе этот цвет означает отрицание и отказ. Черный в первой половине ряда говорит о протесте существующего положения, неразумном бунте против определенных жизненных обстоятельств. Если черный стоит вторым, важно отметить, какой цвет занимает первое место. Например, соседство черного и желтого на первых местах означает стремление к резким переменам, которые призваны улучшить текущее положение.
На восьмом месте черный располагают те, кто стремится сохранять контроль над собственными решениями и действиями.
Отметим, что восьмицветовой тест Люшера имеет подробную и глубокую расшифровку, поэтому для более точных результатов его целесообразно проводить онлайн. Например, здесь.
Плюсы: любимый цвет мы выбираем на уровне подсознания и дать социально желаемый ответ крайне трудно.
Недостатки: требует времени для подробной расшифровки результатов.
Тест не отражает на 100% личность соискателя, но может использоваться, как дополнительный опросник.
Тест на честность
Еще один интересный и быстрый тест используют менеджеры некоторых крупных компаний. Он позволяет проверить кандидата на смелость и честность.
Как провести? В конце собеседования HR-специалисты просят оценить их интервьюера по десятибалльной шкале.
Интерпретация результатов. Ответ соискателя может многое рассказать о его личности. Например, 10 баллов обычно ставят льстецы, а 1 — критики. Объективной оценкой будет цифра от 6 до 9, если, конечно, рекрутер не провалил собеседование.
Плюсы: в этом тесте, кандидат демонстрирует умение соединять в себе смелость и дипломатичность, давая откровенный ответ.
Недостатки: соискатели все равно стараются дать социально желаемый ответ.
Когда необходимо использовать быстрые тесты?
Если у рекрутера в силу различных обстоятельств нет возможности подготовить полноценный опросник, то быстрые тесты могут частично заменить его и дать необходимые результаты.
Стоит помнить, что такие психологические тесты не направлены на выявление необходимых компетенций, а дают информацию о личности в целом. Результаты желательно подтверждать другими опросами, проведенными на следующем этапе собеседования, поскольку, из-за распространенности этих тестов, соискатели могут давать ответы, которые вы хотели бы от них услышать.
Что такое геометрические фигуры? Определение, типы, свойства, факты
Геометрические фигуры Определение
Геометрические фигуры — это замкнутые фигуры, созданные с использованием точек, отрезков, окружностей и кривых. Такие формы можно увидеть повсюду вокруг нас.
Примерами геометрических фигур являются круг, прямоугольник, треугольник и т. д. Пицца круглая, а ее ломтики треугольные. Точно так же двери и окна являются примерами прямоугольников.
У правильной формы все стороны равны. Например, квадрат или правильный шестиугольник. Неправильные формы имеют стороны разной величины. Например, разносторонний треугольник.
Некоторые из наиболее популярных фигур описаны ниже:
- Прямоугольник
Прямоугольник — это фигура, полученная в результате соединения четырех разных точек четырьмя разными линиями. В прямоугольнике противоположные стороны параллельны и равны по длине. Все углы в прямоугольнике прямые. Отличие прямоугольника от квадрата в том, что в прямоугольнике два параллельных отрезка длиннее двух других, а в квадрате все отрезки имеют одинаковую длину.
Примерами прямоугольных объектов являются экраны ноутбуков, мобильные экраны и т. д.
- Квадрат
Квадрат — это четырехсторонняя геометрическая фигура, образованная соединением четырех отрезков прямой равной длины. Подобно прямоугольнику, отрезки, образующие квадрат, лежат под прямым углом друг к другу. Примерами квадратных объектов являются кубик Рубика, игральные кости, шахматные доски и т. д.
- Круг
Круг — это геометрическая фигура, состоящая из прямых линий.
Можно считать, что окружность составлена из бесчисленных точек, расположенных на одинаковом расстоянии от центральной точки.
Примерами круглых объектов являются целые пиццы и колеса.
- Треугольник
Треугольник состоит из трех соединенных отрезков. Это сложная геометрическая фигура, поскольку она может иметь переменные углы и размеры.
Примерами треугольных объектов являются кусочки пиццы, начос, праздничные шапочки и т. д.
Примечательно, что название треугольника меняется в зависимости от его углов и размера сторон. Например, когда два отрезка треугольника образуют прямой угол, такой треугольник называется прямоугольным. Вот как это выглядит:
Любой треугольник с углами меньше 90 градусов называется остроугольным. Точно так же треугольник с одним углом больше 90 градусов называется тупоугольным треугольником. В равноугольном треугольнике все внутренние углы равны 60 градусов, а все стороны равны по длине.
Обратитесь к диаграмме ниже, чтобы лучше понять.
Применение геометрических фигур в реальной жизни
Геометрия — это изучение формы и пространства. Это помогает нам понять другие математические концепции, а также приложения в реальной жизни. Геометрию можно использовать для проектирования зданий, мостов, автомобилей и даже одежды. Принципы геометрии также используются в других разделах математики, таких как тригонометрия и исчисление.
Ниже приведены некоторые из реальных применений:
Квадраты: Квадраты можно найти в природе, например, кристаллы квадратной формы. Квадраты также используются в искусстве. Ярким примером является известная картина Пита Мондриана «Композиция с красным, синим и желтым».
Прямоугольники: Многие искусственные объекты, такие как телевизоры, книги и компьютерные мониторы, имеют прямоугольную форму. Есть много реальных примеров прямоугольников, таких как банкноты, сотовые телефоны и обложки книг.
Круги: Круги можно увидеть повсюду вокруг нас, от пиццы, которую мы едим, до циферблата часов.
Треугольники: Треугольники можно найти во многих местах. Большинство крыш имеют треугольную форму, называемую фронтонами. Треугольники могут помочь поддерживать такие конструкции, как мосты и здания. Есть даже некоторые чипы, которые имеют форму треугольников.
Овалы/эллипсы: Овал или эллипс представляет собой вытянутый круг (яйцевидной формы), длина которого больше ширины.
Примеры трехмерных фигур
Трехмерные фигуры представляют собой группу вершин, линии, соединяющие вершины, и грани, заключенные в эти линии. Они имеют длину, ширину и высоту и занимают некоторый объем. Для многих трехмерных фигур грани двумерны. Кроме того, некоторые фигуры в трех измерениях имеют криволинейные поверхности.
В трех измерениях основными фигурами являются:
- Кубик: Кубик Рубика, кубик сахара
- Конус: Конус для мороженого, пирамидка
- Прямоугольный куб: Деревянная прямоугольная коробка, спичечный коробок
- Цилиндр: Рулон туалетной бумаги; банка газировки
- Сфера: Футбол, Баскетбол
Решаемые примеры
Пример 1.
Сколько сторон у десятиугольника?
Решение : У десятиугольника десять сторон и десять вершин.
Пример 2: Как называется треугольник, у которого только две равные стороны?
Решение : Треугольник, у которого только две равные стороны, называется равнобедренным.
Пример 3: конус имеет двумерную или трехмерную форму?
Решение : Конус представляет собой трехмерную фигуру.
Практические задачи
1
Квадрат имеет _________.
Две равные стороны
Четыре равные стороны
Четыре неравные стороны
Ни одна из этих
Правильный ответ: Четыре равные стороны
Квадрат в геометрии — это плоская фигура, имеющая четыре равные стороны и четыре прямых угла.
2
Расстояние от центра круга до его внешней границы называется _________.
радиус
кривая
диаметр
хорда
Правильный ответ: радиус
Расстояние от центра круга до его внешней границы называется радиусом круга. Диаметр круга всегда вдвое больше его радиуса.
3
Куб — это _________.
одномерная фигура
трехмерная фигура
двумерная фигура
Ничего из этого
Правильный ответ: трехмерная фигура
Куб – это трехмерная фигура. У него шесть граней, восемь вершин и двенадцать ребер. Каждая грань куба представляет собой квадрат, и все ребра имеют одинаковую длину. У куба шесть квадратных граней.
4
Равносторонний треугольник _________.
открытая форма
неправильная форма
правильная форма
замкнутая кривая
Правильный ответ: правильная форма
Стороны равностороннего треугольника имеют одинаковую длину. Итак, равносторонний треугольник – это правильная фигура.
Заключение
Геометрические фигуры являются частью нашей повседневной жизни. Учащимся они помогают заложить основу для более сложных понятий, таких как пространственные отношения.
Часто задаваемые вопросы
Какие основные геометрические фигуры?
Основными геометрическими формами являются круг, квадрат, прямоугольник, треугольник и т. д. Эти формы могут быть расположены в различных комбинациях.
Как образуются геометрические фигуры?
Геометрические фигуры формируются с помощью линий, точек или кривых. Мы должны помнить, что эти формы должны соответствовать математическому определению. Если форму нельзя определить математически, она не является геометрической.
Какие примеры фигур не являются геометрическими?
В природе можно найти негеометрические формы. Например, галька, реки и т. д.
Как определить многоугольник?
Многоугольник — это фигура, состоящая из прямых линий без кривых.
У него нет открытых сторон. «Многоугольник» — это широкий термин, обозначающий различные формы, такие как квадраты, треугольники и прямоугольники.
9 наиболее распространенных форм и способы их идентификации
Вы, вероятно, многое узнали о формах, даже не задумываясь о том, что они из себя представляют. Но понимание того, что такое форма, невероятно удобно при сравнении ее с другими геометрическими фигурами, такими как плоскости, точки и линии.
В этой статье мы рассмотрим, что такое фигура, а также несколько распространенных форм, как они выглядят и основные формулы, связанные с ними.
Что такое форма?
Если кто-нибудь спросит вас, что такое форма, вы, вероятно, сможете назвать несколько из них. Но «форма» имеет и особое значение — это не просто название кругов, квадратов и треугольников.
Форма — это форма объекта, а не то, сколько места он занимает или где он находится физически, а реальная форма, которую он принимает.
Круг определяется не тем, сколько места он занимает или где вы его видите, а скорее фактической круглой формой, которую он принимает.
Фигура может быть любого размера и появляться где угодно; они ничем не ограничены, потому что фактически не занимают места. Это довольно сложно уловить, но не думайте о них как о физических объектах — форма может быть трехмерной и занимать физическое пространство, например, пирамидальная подставка для книг или цилиндрическая банка из-под овсяных хлопьев, или может быть двухмерным и не занимать физической комнаты , например треугольник, нарисованный на листе бумаги.
Тот факт, что он имеет форму, отличает форму от точки или линии.
Точка — это просто позиция; у него нет ни размера, ни ширины, ни длины, ни какого бы то ни было измерения.
Линия, напротив, одномерна. Он простирается бесконечно в любом направлении и не имеет толщины. Это не форма, потому что у нее нет формы.
Хотя мы можем представлять точки или линии в виде фигур, потому что нам нужно их видеть, на самом деле они не имеют никакой формы.
Вот что отличает форму от других геометрических фигур — она двумерна или трехмерна, потому что имеет форму.
Кубы, подобные тем, что показаны здесь, представляют собой трехмерные формы квадратов — и то, и другое — формы!
6 основных типов двумерных геометрических фигур
Трудно изобразить форму только на основе определения— что значит иметь форму , но не занимать место? Давайте рассмотрим несколько различных форм, чтобы лучше понять, что именно означает быть формой!
Мы часто классифицируем фигуры по количеству сторон. «Сторона» — это отрезок линии (часть линии), который составляет часть фигуры. Но у фигуры тоже может быть неоднозначное количество сторон.
Тип 1: Эллипсы
Эллипсы представляют собой круглые овальные формы, в которых заданная точка ( p ) имеет одинаковую сумму расстояний от двух разных фокусов.
Овал
Овал немного похож на смазанный круг — он не совсем круглый, а как-то вытянут.
Однако классификация неточная. Есть много, много видов овалов, но общее значение состоит в том, что они имеют круглую форму, которая является удлиненной, а не идеально круглой, как круг. Овал — это любой эллипс, фокусы которого находятся в двух разных положениях.
Поскольку овал не идеально круглый, формулы, которые мы используем для их понимания, должны быть скорректированы.
Также важно отметить, что вычисление длины окружности довольно сложно, поэтому ниже нет уравнения длины окружности. Вместо этого используйте онлайн-калькулятор или калькулятор со встроенной функцией измерения окружности, потому что даже самые лучшие уравнения окружности, которые вы можете составить вручную, являются приблизительными.
Определения
- Большой радиус : расстояние от начала овала до самого дальнего края
- Малый радиус : расстояние от начала овала до ближайшего края
Формулы
- Площадь = $\Major \Radius*\Minor \Radius*π$
Круг
Сколько сторон у круга? Хороший вопрос! К сожалению, хорошего ответа нет, потому что «стороны» имеют больше общего с многоугольниками — двумерной формой, по крайней мере, с тремя прямыми сторонами и, как правило, по крайней мере с пятью углами.
Наиболее знакомые нам фигуры — это многоугольники, но у кругов нет прямых сторон и явно не хватает пяти углов, поэтому они не являются многоугольниками.
Итак, сколько сторон у круга? Нуль? Один? На самом деле это не имеет значения — вопрос просто не относится к кругам.
Круг — это не многоугольник, но что это такое? Окружность — это двумерная фигура (у нее нет толщины и глубины), состоящая из кривой, которая всегда находится на одном и том же расстоянии от точки в центре. Овал имеет два фокуса в разных положениях, тогда как фокусы круга всегда находятся в одном и том же положении.
Определения
- Начало: центр окружности
- Радиус: расстояние от начала координат до любой точки на окружности
- Окружность: 92$
Тип 2: Треугольники
Треугольники — простейшие многоугольники.
У них три стороны и три угла, но они могут отличаться друг от друга. Возможно, вы слышали о прямоугольных или равнобедренных треугольниках — это разные типы треугольников, но все они имеют три стороны и три угла.
Поскольку существует много видов треугольников, существует лотов важных формул треугольника , многие из них сложнее других. Основы приведены ниже, но даже основы основаны на знании длины сторон треугольника. Если вы не знаете стороны треугольника, вы все равно можете вычислить его различные аспекты, используя углы или только некоторые из сторон.
Определения
- Вершина : точка пересечения двух сторон треугольника
- Основание : любая из сторон треугольника, обычно нижняя сторона
- Высота : расстояние по вертикали от основания до вершины, с которой оно не связано
Формулы
- Площадь = ${\основание*\высота}/2$
- Периметр = $\сторона a + \сторона b + \сторона c$
Тип 3: Параллелограммы
Параллелограмм — это фигура с равными противоположными углами, параллельными противоположными сторонами и параллельными сторонами одинаковой длины.
Вы могли заметить, что это определение применимо к квадратам и прямоугольникам, потому что квадратов и прямоугольников также являются параллелограммами ! Если вы можете вычислить площадь квадрата, вы можете сделать это с любым параллелограммом.
Определения
- Длина : мера нижней или верхней стороны параллелограмма
- Ширина : мера левой или правой стороны параллелограмма
Формулы
- Периметр : $\Сторона 1 + \Сторона 2 + \Сторона 3 + \Сторона 4$
- Альтернативно, Периметр : $\Side*4$
Прямоугольник
Прямоугольник — это фигура с параллельными противоположными сторонами и всеми углами в 90 градусов. Как тип параллелограмма, он имеет противоположные параллельные стороны.
В прямоугольнике один набор параллельных сторон длиннее другого, что делает его похожим на вытянутый квадрат.
Поскольку прямоугольник является параллелограммом, вы можете использовать те же самые формулы для вычисления его площади и периметра.
Квадрат
Квадрат очень похож на прямоугольник, за одним заметным исключением: все его стороны имеют одинаковую длину. Как и прямоугольники, квадратов имеют все углы 90 градусов и параллельны противоположным сторонам. Это потому, что квадрат на самом деле является типом прямоугольника, который является типом параллелограмма!
По этой причине вы можете использовать те же формулы для вычисления площади или периметра квадрата, что и для любого другого параллелограмма.
Ромб
Как вы уже догадались, ромб — это разновидность параллелограмма. Отличие ромба от прямоугольника или квадрата в том, что его внутренние углы только такие же, как и их диагональные противоположности.
Из-за этого ромб немного похож на квадрат или прямоугольник, немного скошенный в сторону . Хотя периметр вычисляется таким же образом, это влияет на способ вычисления площади, поскольку высота уже не такая, как в квадрате или прямоугольнике.
Определение
- Диагональ : длина между двумя противоположными вершинами
Формулы
- Площадь = ${\Диагональ 1*\Диагональ 2}/2$
Тип 4: Трапеции
Трапеции — четырехсторонние фигуры с двумя противоположными параллельными сторонами. В отличие от параллелограмма, трапеция имеет только две противоположные параллельные стороны, а не четыре , что влияет на способ вычисления площади и периметра.
Определения
- Основание : любая из параллельных сторон трапеции
- Ноги : любая из сторон трапеции непараллельна
- Высота : расстояние от одной базы до другой
Формулы
- Площадь : $({\Base_1\length + \Base_2\length}/2)\altitude$
- Периметр : $\Base + \Base + \Leg + \Leg$
Тип 5: Пятиугольники
Пятиугольник — это пятиугольник.
Поскольку форма более сложная, ее необходимо разделить на меньшие фигуры, чтобы вычислить ее площадь.
Определения
- Апофема : линия, проведенная из центра пятиугольника к одной из сторон, пересекающая сторону под прямым углом.
Формулы
- Периметр : $\Сторона 1 + \Сторона 2 + \Сторона 3 + \Сторона 4 + \Сторона 5$
- Площадь : ${\Perimeter*\Apothem}/2$
Тип 6: Шестиугольники
Шестиугольник — это шестиугольник, очень похожий на пятиугольник.
Чаще всего мы видим правильные шестиугольники, но они, как и пятиугольники, также могут быть неправильными, выпуклыми или вогнутыми.
Также как и пятиугольники, формула площади шестиугольника значительно сложнее, чем у параллелограмма.
Формулы
- Периметр : $\Сторона 1 + \Сторона 2 + \Сторона 3 + \Сторона 4 + \Сторона 5 + \Сторона 6$
- Площадь : ${3√3*\Сторона*2}/2$
- В качестве альтернативы, Область : ${\Perimeter*\Apothem}/2$
Как насчет трехмерных геометрических фигур?
Существуют также трехмерные формы, которые имеют не только длину и ширину, но и глубину или объем. Это формы, которые вы видите в реальном мире, например, сферический баскетбольный мяч, цилиндрический контейнер с овсянкой или прямоугольная книга.
Трехмерные фигуры, естественно, более сложны, чем двумерные, с дополнительным измерением — количеством места, которое они занимают, а не только формой, — которое необходимо учитывать при расчете площади и периметра.
Математика, включающая 2D-формы, такие как приведенные выше, называется плоскостной геометрией, поскольку она имеет дело конкретно с плоскостями или плоскими формами .
Математика, связанная с трехмерными формами, такими как сферы и кубы, называется твердотельной геометрией, потому что она имеет дело с твердыми телами, другим словом для трехмерных форм .
2D-формы составляют 3D-фигуры, которые мы видим каждый день!
3 основных совета по работе с фигурами
Существует так много типов фигур, что бывает сложно запомнить, какие из них есть какие, и как вычислить их площади и периметры. Вот несколько советов и приемов, которые помогут вам их запомнить!
#1: определение многоугольников
Некоторые фигуры являются многоугольниками, а некоторые нет. Один из самых простых способов определить, к какому типу формы относится предмет, – выяснить, является ли он многоугольником.
Многоугольник состоит из прямых линий, которые не пересекаются. Какие из фигур ниже являются многоугольниками, а какие нет?
Круг и овал не являются многоугольниками, а значит, их площадь и периметр вычисляются по-разному.
Узнайте больше о том, как вычислить их, используя $π$ выше!
#2: Проверка на наличие параллельных сторон
Если фигура, на которую вы смотрите, является параллелограммом, обычно проще вычислить его площадь и периметр, чем если это не параллелограмм. Но как определить параллелограмм?
В названии указано — параллельно. Параллелограмм представляет собой четырехугольник с двумя наборами параллельных сторон . Квадраты, прямоугольники и ромбы являются параллелограммами.
Квадраты и прямоугольники используют одни и те же базовые формулы для площади — длину, умноженную на высоту. Для них также очень легко найти периметр, так как вы просто складываете все стороны вместе.
С ромбами дело обстоит сложнее, потому что вы перемножаете диагонали и делите на два.
Чтобы определить, на какой вид параллелограмма вы смотрите, спросите себя, имеет ли он все углы по 90 градусов.
Если да, то это либо квадрат, либо прямоугольник .
