Триметрия 2: Три метра над уровнем неба 2: Я тебя хочу

описание, содержание, интересные факты и многое другое о фильме

Фильм Три метра над уровнем неба: Я тебя хочу

2012

1 ч. 58 мин.

16+

Мелодрамы

Драмы

Зарубежные

Развернуть трейлер

Бесплатные фильмы

Трейлер

2012

1 ч. 58 мин.

16+

Мелодрамы

Драмы

Зарубежные

Бесплатные фильмы

Марио Касас и Мария Вальверде в сиквеле нашумевшей драмы Фернандо Гонсалеса Молины. События фильма «Три метра над уровнем неба. Я тебя хочу», который мы предлагаем посмотреть онлайн, развиваются уже после возвращения Аче из Лондона. И вновь в центре сюжета — запутанные отношения, поиски себя, встречи и расставания. С момента разрыва Аче и Баби прошло уже два года. Вернувшись в Барселону, он боится встретить ее, ведь все это время жил воспоминаниями о прошлом. Однако дома Аче понимает, что не стоит оглядываться назад и нужно начать все заново.

Пытаясь заглушить боль и периодически появляющиеся отголоски памяти, он ищет и находит новую работу, новых друзей и новую любовь. Красотка Джин будит в душе Аче чувства, которые он испытывал только с Баби, несмотря на то, что девушки совершенно разные. Кажется, ему снова удалось подняться на те самые три метра над уровнем неба. Но все меняется, когда он случайно сталкивается с Баби. Сможет ли Аче пережить эту встречу и найти в себе силы идти дальше?

Рейтинг Иви

Интересный сюжет

Бесплатные фильмы

Колье для снежной бабы

В плену обмана

Счастливый шанс

Тихий центр

Чужие дети (2020)

Пробуждение любви

Снежная любовь, или Сон в зимнюю ночь

Я никогда не плачу

Привычка расставаться

Пока живу, люблю

Лучше всех

Звезда

Влюбленные

Два сердца

Вместо нее

Бабушка на сносях

Ветреная женщина

Деревенская комедия

Формула счастья

День Святого Валентина

Любит не любит

Татьянин день

Джамайка

Карина Красная

Фернандо

Гонзалез Молина

Марио

Касас

Мария

Вальверде

Клара

Лаго

Альваро

Сервантес

Андреа

Дуро

Диего

Мартин

Марина

Салас

Антонио

Веласкез

Нереа

Камачо

Трейлер (дубляж)

2 мин.

Фильмы про настоящую любовь

Романтические фильмы

Фильмы, снятые на основе книг

Фильмы с субтитрами

Фильмы про любовные треугольники

Аче, после двух лет проживания в Лондоне, решает возвратиться в родные пенаты, не смотря на то, что мысли о Баби до сих пор не дают ему покоя. Он решает начать все с чистого листа, озаботиться поиском работы, новых друзей, и, возможно, новых отношений. В аэропорту Аче встречает его любимый старший брат, который за это время успел нажить немалое состояние, тогда как для самого Аче мало что изменилось: он все еще возвращается в своих мыслях к прошлому, и никак не может начать жить настоящим. Помимо бесконечных размышлений о Баби, его сильно мучают воспоминания о своем погибшем друге, с чьей смертью Аче никак не может смириться.

Прибыв домой, Аче решает прокатиться на своем старом мотоцикле, и заодно, повстречаться с любимыми друзьями. На заправке Аче при забавных обстоятельствах знакомится с девушкой по имени Джин – она пытается слить с его мотоцикла немного бензина, чтобы заправить свою машину. Позабавленный Аче сам садится за руль ее автомобиля, чтобы как следует ее припугнуть, но не тут-то было – Джин отчаянная девушка не робкого десятка.

Через день Аче устраивается на работу в телешоу по поиску талантов, и там он снова встречает свою новую знакомку – сумасшедшую Джин, которая, помимо резкого характера, обладает некоторыми способностями: она неплохо танцует и поет. Аче кажется, что он влюбляется в эту необычную дикарку, и на какой-то момент, он даже забывает о своих прошлых чувствах к Баби.

Но вскоре судьба подкидывает Аче старое испытание на новый лад – он снова встречает Баби, и понимает, что его чувства к ней просто уснули на какое-то время, но все еще не угасли. Однако, он узнает, что Баби вскоре выходит замуж, тогда как сам Аче все еще не может понять, кто же ему важнее – милая и веселая Джин, которая возродила его к жизни, или же Баби, с которой ему было так хорошо когда-то. Аче предстоит сделать нелегкий выбор, между призрачным прошлым, и прекрасным и радостным настоящим.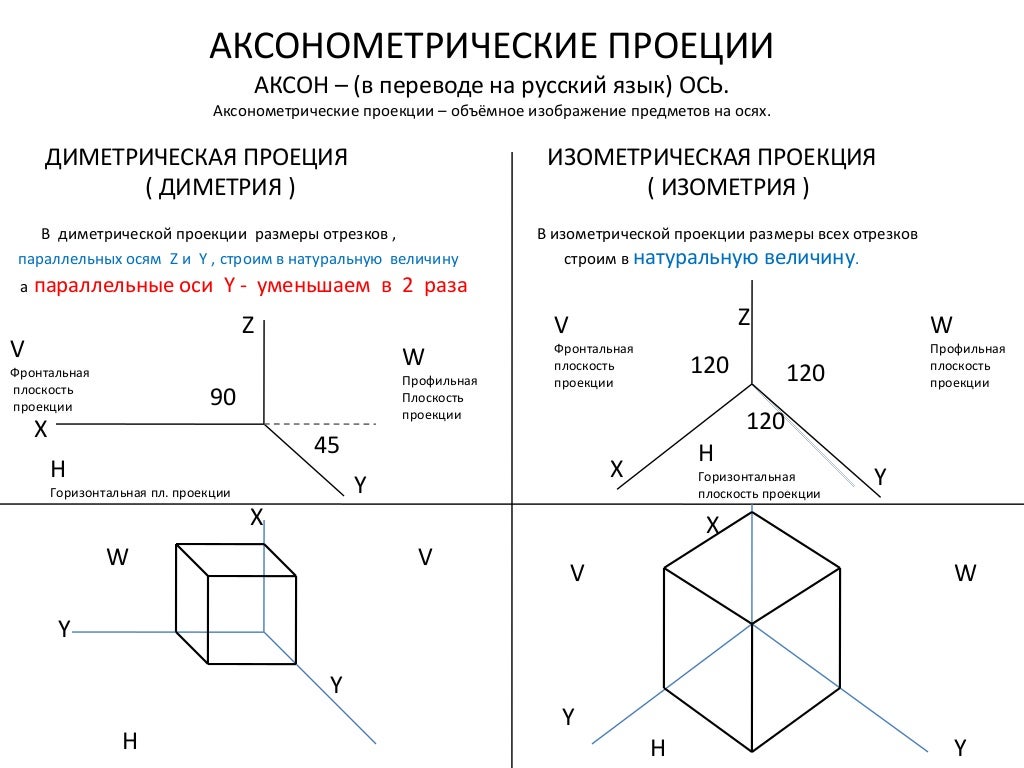

Асель

Все равно хочу союз Бади и Ачи.У них любовь чистая!

10 февраля 2018

serikov.evgeny

Фильм хороший мне понравился. Лучше не ставили вторую особу а только Баби одну и Ачи через 2 года прожитое в лондоне вернулся и любил Баби мог остаться с ней! Вот какая должна концовка быть!

30 декабря 2012

Лера

Мне одной на протяжении всей второй части было больно, и не приятно смотреть на пару Аси и Джина. Баби была милой, женственной девушкой, а эта пацанка мерзкая. Я ждала хеппи энд с Баби но увы.

20 июня 2019

Ольга

фильм хороший…обычно когда снимают продолжение, уже изначально понимаешь, что будет не интересно…а тут я не могла оторваться от просмотра…в этой части меня разочаровала БАБИ…Джин и Ачи более похожи по темпераменту…СУПЕР…

16 июля 2013

olerlik

Невероятно красивые саундтреки к фильмам, что к первой, что ко второй части. Обалденная игра актеров, все абсолютно, как главных, так и второстепенных, невероятное мастерство режиссеров и операторов.

Уже неделю, как помешанная смотрю обе части каждый день. Фильм удивительно сочетал в себе харизматичных, красивых, интересных актеров, живописные декорации-пейзажи и мастерство режиссеров-постановщиков. Ради любопытства решила посмотреть итальянскую версию, не смогла — это небо и земля. Аче напомнил Бодрова младшего, Джейкоба из Сумерек, такой же одновременно мужественный и какой-то по детски добрый, наивный что ли. Короче, фильм прицельно бьет по самым чувственным струнам женской души.

27 октября 2013

irenka888

Ни минуты не пожалела о просмотре. Фильм достойный. Рекомендую своим друзьям.

25 февраля 2014

lena.ryazantseva

Мужчины чувствовать умеют. А, следовательно, они… люди?!!!)))

28 августа 2015

Iskork8

Прекрасный фильм…Однозначно смотреть!!!

9 декабря 2012

olerlik

Странно перевели название фильма, должно быть не «я хочу тебя», а «я хочу быть с тобой» — два совершенно разных смысла. Вторая часть неразрывна с первой и на том же уровне — 10 из 10-ти.

Без последней встречи главных героев еще было не понятно, что да как, а тут все встало на свои места: два раза в одну реку не войдешь. Можно было бы сказать, что Баби дура, все испортила, когда порвала с Аче, но она не могла по-другому, она иная, и он не смог бы измениться. В итоге, если бы они остались вместе, наверняка разрыв все равно бы произошел, рано или поздно. А тут она не выдержала последнего испытания смертью друга.

27 октября 2013

николай

Молодость проходит и мы признаем свои шибки становимся умнее,мудрее с годами.

5 декабря 2012

Кэтрин

Да,фильм, однозначно, хороший. Время идет… Мы взрослеем… И начинаем хоть что- то понимать в этой жизни.

11 января 2014

Олеся

Все бы ничего, только вот не пойму — в Испании красивые девушки закончились?

1 мая 2019

• Клара Лаго, сыгравшая Джин, должна была стать Баби еще в первом фильме, но утвердили Марию Вальверде
• Во время съемок ходили слухи, что у Марио Касаса и Клары Лаго завязался роман, однако вскоре оказалось, что эта информация была частью пиар-кампании
• Кассовые сборы фильма в России в два раза превысили сборы «Сумерек»
• Когда снималась эротическая сцена на крыше, температура воздуха приближалась к нулю, в связи с чем оператору приходилось искать выгодные ракурсы, при которых не видно гусиной кожи на телах актеров
• После съемок Марио Касас стал замечать, что часто ведет себя в реальной жизни, как Ачи, что порой настораживает его близких
• Марио Касас большой поклонник Ван Дама, из фильмов которого он позаимствовал некоторые приемы в драках и манеру съемок в экшн сценах
• В сцене, где Аче только знакомится с Джин, он садится в ее машину, после чего Джин пристегивается. Однако, после того, как Аче делает резкий поворот, видно, что Джин резко падает к нему на колени, и ремень безопасности уже отстегнут.
• После падения Аче в воду вместе с мотоциклом, Аче выплывает на берег, и начинает звонить по мобильнику, который нисколько не намок и абсолютно исправен.

Приложение доступно для скачивания на iOS, Android, SmartTV и приставках

Подключить устройства

правила, советы, ошибки — Gamedev на DTF

Изометрия — один из самых популярных вариантов отображения игрового мира, особенно на рынке мобильного геймдева. Разбираемся, как с ней работать.

14 872 просмотров

Автор: Duncan Bell

Что такое изометрия и зачем она нужна

Изометрия — этот способ изображать предметы без перспективных искажений. В отличие от классической реальной перспективы, где удаленные от зрителя предметы кажутся меньше, в изометрии предметы на разном расстоянии остаются одинакового размера.

Перспектива (а) и изометрия (б)

Существует несколько видов изометрии: прямоугольная, косоугольная фронтальная, косоугольная горизонтальная. Они различаются положением осей X и Y и углами между ними. От этих параметров зависит изображение предмета. Это хорошо видно на примере с кубиком:

Прямоугольная (а), косоугольная фронтальная (б) и косоугольная горизонтальная (в) изометрические проекции

Чаще всего, говоря об изометрии, подразумевают прямоугольную изометрическую проекцию. В ней ось Z направлена вертикально, а оси XYZ образуют углы в 120°. Выглядит это так:

Кроме изометрии и ее разновидностей, существуют похожие на нее диметрия и триметрия. В изометрии углы между осями XYZ одинаковые и равны 120°, в диметрии равны два из трех углов, в триметрии величина всех углов между осями разная. Все виды этих проекций нашли применение в геймдеве, их привычно называют одним словом — изометрия.

Примеры проекций, используемых в играх. Источник

Например, в игре Invisible, Inc. используется изометрическая проекция с углами 120°:

Источник

Игра Transistor — пример использования диметрии в игровой графике:

Источник

В игре Simcity 4 используется триметрическая проекция:

Источник

На заре становления изометрия позволяла создавать в играх имитацию объемного пространства с помощью плоских спрайтов. Так как объекты не меняют своих размеров в зависимости от расположения на игровом поле, компьютеру не нужно производить сложные вычисления и моделировать постоянно меняющееся окружение.

Примеры первых изометрических игр — это Zaxxon от Sega (1982), Treasure Island (1981), Q*bert (1982).

Сегодня, когда компьютеры с легкостью справляются с воспроизведением сложной графики, изометрия по-прежнему остается актуальной. За последние несколько лет вышли такие изометрические игры как Invisible, Inc, Transistor, Disco Elysium и многие другие.

Стильная ролевая игра Disco Elysium — отличный пример современной игровой изометрии. Источник

Художественный стиль Shadowrun Returns описывают как совмещающий 2D и 3D. Источник

Изометрия остается популярной в RPG и стратегиях и повсеместно встречается в мобильных играх. Она оставляет разработчикам пространство для экспериментов и в создании визуала, и в разработке геймплея.

Mobile Legends: Bang Bang — одна из популярнейших MOBA-игр в мире. Источник

Как рисовать изометрию

Строим изометрическую сетку

В рисовании изометрии главную роль играет сетка, относительно которой художник будет выстраивать все объекты. Это может быть как классическая изометрическая сетка с углами между осями 120°, так и эксклюзивная для определенного проекта — параметры сетки могут определяться техническим заданием или самим художником.

Стандартная изометрическая сетка с углами 120°

Изометрия — отличный вариант для тех, кто не любит ломать голову над перспективными сокращениями. Нарисовав сетку один раз, вы ориентируете все горизонтали в рисунке к параллели с этой сеткой, а вертикали оставляете без изменений.

Небольшая геометрическая композиция, выстроенная по изометрической сетке. Видно, что рёбра лежат параллельно линиям сетки.

Стандартный вариант игровой изометрической сетки — диметрия с соотношением сторон 2:1.

Кадр из видео

Существует множество способов создания изометрической сетки. Можно отрисовать ее вручную, можно взять шаблон из интернета, можно настроить направляющие в Photoshop.

Один из простых и быстрых способов — строим сетку с углами 90°:

Поворачиваем ее на 45°, нажимаем «применить»:

Затем отключаем привязку высоты к ширине и меняем высоту со 100% на 50%. В итоге получится сетка с соотношением сторон 2:1, часто используемая в изометрических проектах:

Процент высоты можно менять в зависимости от художественной задачи. В результате будет меняться раскрытие сетки

Важно отметить, что, чем больше сетка раскрыта, тем лучше будут видны объекты (одни не будут загораживать другие), но при этом мы можем показать меньше игрового поля. И наоборот, при небольшом раскрытии сетки видно больше игрового пространства, но объекты могут наползать друг на друга. Учитывайте этот нюанс при выборе угла сетки.

Диметрическая сетка и сетка с меньшим углом раскрытия

Строим простые фигуры по сетке

Рисование начинается с построения базовых форм. Изометрия не исключение. Ориентируемся на сетку и строим примитивные фигуры.

Если с квадратами, прямоугольниками треугольниками все понятно — их необходимо просто вписать в необходимое количество плиток, то как быть с кругом?

В случае с кругом нужно следить, чтобы крайние точки окружности с каждой стороны совпадали с углами квадратов как на картинке (отмечены точками):

Если ориентироваться по точкам сложно, можно провести через центр окружности два отрезка — своеобразную крестовину — и, ориентируясь по ней, масштабировать круг до нужных пропорций, чтобы крестовина совпала с сеткой.

Строим объемные фигуры по сетке

Переходим к объемным фигурам. На основе квадрата строим куб. Копируем квадрат в основе на две клетки вверх и соединяем углы вертикалями. С помощью оттенков можно показать объем.

Подобным образом строим параллелепипед на основе прямоугольника.

Пирамиду также довольно легко построить на основе квадрата или прямоугольника. Проводим вертикаль из центра основания на нужную высоту и от вершины проводим прямые к углам — ребра пирамиды.

В основании цилиндра и конуса лежит круг. Копируем круг основания на нужную высоту и соединяем края вертикалями — получится цилиндр.

Проводим из центра вертикаль на нужную высоту, находим вершину и от нее проводим наклонные линии к краям круга. Получится конус.

Освоившись с базой, можно переходить к более сложным формам.

Прежде чем приступать к непосредственно построению в изометрии, пробуйте сначала свободно поскетчить, не ограничивайте воображение. Когда найдете нужную форму — переходите к построению по сетке.

Домик в изометрии

Классический кейс казуальных игр — изометрический домик. Разбиваем концепт на простые формы и отстраиваем по сетке.

Начинаем с болванки параллелепипеда — основания домика. Его довольно легко построить по изометрической сетке.

Переходим к крыше. Проводим вертикали одинаковой длины по центрам меньших граней — получатся центральные оси, относительно которых будем строить крышу. Параллельно сетке проводим между этими осями конёк, а также боковые свесы. Соединяем свесы с коньком, чтобы получить скаты крыши.

Относительно оси строим дверь и окно. На скате крыши также строим центральную ось, опираясь на нее рисуем слуховое окошко. Вертикали остаются вертикальными, горизонтали строим по сетке.

Рисуем толщину стен в оконных проемах, добавляем детали.

Отметим, что в данном примере относительно центральных осей в обе стороны отложено одинаковое расстояние частей домика. На начальных этапах обучения так проще ориентироваться в построении и деталях.

Небольшое отступление: не всегда детали расположены симметрично относительно центральной оси, есть и примеры с асимметрией. Но чаще всего в геймдеве мы встречаем примеры симметричного построения объектов.

Завершаем лайн, добавляя финальные штрихи и детали, говорящие о характере домика.

Внутреннее убранство домика тоже можно построить примитивами по сетке, а затем дополнить мелочами.

Бэкграунд и окружение играют важную роль в изометрических играх — пользователь видит все игровое пространство или бОльшую его часть. Уделите этому особое внимание.

Дерево в изометрии

Органические объекты (деревья, кусты, камни и т.п.) с одной стороны проще нарисовать в изометрии, так как это плавные формы и там почти нет таких строгих построений. Но с другой стороны, в их изображении проще запутаться.

В этом примере в основании ствола дерева — окружности разных размеров.

Простраиваем ствол и ветки. Важно, чтобы дерево вписывалось в 3D-пространство, чтобы ветки и крона вокруг ствола была направлены во все части света почти сферически. Поэтому, чтобы сделать дерево более объемным, направляем ветви вдоль разных линий сетки.

Простыми формами намечаем крону.

Детализируем дерево, дополняем его листьями и корнями, также направляя их в разные стороны.

Завершаем рисунок деталями.

Персонажи в изометрии

Изометрических персонажей тоже рисуют на основании примитивов. В данном случае в основании базовых частей персонажа лежат эллипсы разных размеров.

Важно, чтобы симметричные части фигуры (в данном случае, например, края прически, подол платья) находились на одном уровне. Проверяйте их линиями, параллельными сетке.

Важно следить за соотношением масштабов объектов рисунка: то есть чтобы персонаж помещался в дверь, а не был размером с дом. В этом примере объекты сомасштабны, поэтому выглядят убедительно.

Ошибки в рисовании изометрии

Несколько типичных ошибок художников, начинающих работать с изометрией:

1. Отсутствие внутреннего построения. Это происходит, когда художник берется за детали, прежде чем построить объекты примитивами. В мелочах легко запутаться и можно выбиться из изометрической сетки. Помните: сначала строим простые формы, проверяем их на соответствие сетке, а потом переходим к подробной проработке.
2. Неправильное построение кривых форм. Кривые в изометрии строить несколько сложнее, чем прямые линии. Внимательно следите за правильным построением эллипсов на сетке, за расположением относительно центральной оси.
   
3. Несоответствие объектов одной изометрической сетке. Все нарисованные объекты должны быть ориентированы одинаково. Нельзя в проекте для одних спрайтов применять одну сетку, а для других — другую.
   
4. Разный уровень детализации. Следите, чтобы количество деталей у всех объектов было примерно одинаковым.
   
5. Разница масштабов. Когда художник перестает соотносить объекты рисунка между собой, может получиться, что персонаж станет крупнее домика и не сможет с ним взаимодействовать (пройти в дверь, заглянуть в окно и т.п.) Важно сравнивать размеры персонажей с окружением.
   

Текст написала Стефания Косюг, автор в Smirnov School. Мы готовим концепт-художников, левел-артистов и 3D-моделеров для игр и анимации. Если придёте к нам на курс, не забудьте спросить о скидке для читателей с DTF.

2: Тригонометрия — Математика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

• Идентификатор страницы

  32545

• 2. 1: Единица окружности – функции синуса и косинуса

  В этом разделе мы рассмотрим этот тип вращательного движения по окружности. Для этого нам нужно сначала определить тип круга, а затем поместить этот круг в систему координат. Тогда мы можем обсудить круговое движение в терминах пар координат.

• 2.2: Другие тригонометрические функции

  Тригонометрические функции позволяют нам задавать формы и пропорции объектов независимо от точных размеров. Мы уже определили функции синуса и косинуса угла. Хотя синус и косинус являются наиболее часто используемыми тригонометрическими функциями, есть еще четыре. Вместе они составляют набор из шести тригонометрических функций. В этом разделе мы исследуем остальные функции.

• 2.3: Тригонометрия прямоугольного треугольника

  Ранее мы определили синус и косинус угла через координаты точки на единичной окружности, пересекаемой конечной стороной угла. В этом разделе мы увидим еще один способ определения тригонометрических функций с использованием свойств прямоугольных треугольников.

• 2.4: Решение тригонометрических уравнений с тождествами

  В этом разделе мы начнем изучение основных тригонометрических тождеств, включая то, как мы можем их проверить и как мы можем использовать их для упрощения тригонометрических выражений.

• 2.5: Тождества суммы и разности

  В этом разделе мы изучим методы, которые позволят нам решать полезные задачи. Следующие формулы упростят многие тригонометрические выражения и уравнения. Имейте в виду, что в этом разделе термин «формула» используется как синоним слова «идентичность».

• 2.6: Двойной угол, половинный угол и формулы редукции

  В этом разделе мы исследуем три дополнительные категории тождеств. Тождества двойного угла выводятся из формул суммы основных тригонометрических функций: синуса, косинуса и тангенса. Формулы редукции особенно полезны в исчислении, поскольку они позволяют уменьшить силу тригонометрического члена. Формулы половинного угла позволяют нам найти значение тригонометрических функций, содержащих половинные углы, независимо от того, известен исходный угол или нет.

---

2: Тригонометрия распространяется по незадекларированной лицензии и была создана, изменена и/или курирована LibreTexts.

1. Наверх
• Была ли эта статья полезной?

1. Тип изделия

   Глава

2. Теги

   На этой странице нет тегов.

Решение треугольников SSS

«SSS» означает «Бок, Бок, Бок»

« SSS » — это когда мы знаем три стороны треугольника и хотим найти недостающих углов .




Чтобы решить треугольник SSS: Сначала используйте закон косинусов, чтобы вычислить один из углов затем снова используйте закон косинусов, чтобы найти другой угол и, наконец, используйте углы треугольника, добавленные к 180 °, чтобы найти последний угол.

Мы используем «угловую» версию закона косинусов:

соз(С) = а ² + б ² — в ² 2аб

соз(А) = б ² + в ² − а ² 2бк

соз(В) = в ² + а ² − б ² 2ка

(у всех одинаковая формула, просто разные этикетки)

Пример 1

В этом треугольнике мы знаем три стороны:

• а = 8,
• б = 6 и
• с = 7,

Сначала используйте закон косинусов, чтобы найти один из углов. Неважно, какой. Сначала найдем угол A :

cos(A) = (b ² + c ² − a ² ) / 2bc

cos(A) = (6 ^{1 +} − 8 ² ) / (2×6×7)

cos(A) = (36 + 49 − 64) / 84

cos(A) = 0,25

A = cos ^-1 (0,25)

A = 75,5224…°

A = 75,5224…°

A = 90,25 ° до одного десятичного знака.

Далее находим другую сторону. Мы снова используем закон косинусов, на этот раз для угла B:

cos(B) = (c ² + a ² − b ² )/2ca

cos(B) = (7 ² + 8 ² − 6 ² )/(2×7×8)

cos(B) = (49 + 64 − 36) / 112

cos(B) = 0,6875

B = cos ^-1 (0,6875)

B = 46,5674…°

B = 46,6° угол с точностью до одного знака после запятой. используя «углы треугольника прибавляют к 180°»:

C = 180° − 75,5224…° − 46,5674…°

C = 57,9° с точностью до одного десятичного знака

Теперь мы полностью решили треугольник, т. е. мы нашли все его углы.

В треугольнике могут быть буквы, отличные от ABC:

Пример 2

Это также треугольник SSS.

В этом треугольнике нам известны три стороны: x = 5,1, y = 7,9 и z = 3,5. Сначала найдите угол X с помощью закона косинусов:

cos(X) = (y ² + z ² − x ² )/2yz

cos(X) = ((7.9) ² + (3,5) ² — (5,1) ² )/(2×7,9×3,5)

cos(X) = (62,41 + 12,25 — 26,01)/55,3

cos(X) = 48,65/55,3 0,8797…

X = cos ^-1 (0,8797…)

X = 28,3881…°

X = 28,4° с точностью до одного десятичного знака

Далее мы снова воспользуемся законом косинусов, чтобы найти угол Y:

cos (Y) = (z ² + x ² — y ² )/2zx

cos(Y) = -24,15/35,7 = -0,6764…

cos(Y) = (12,25 + 26,074) − 62,41)/35,7

cos(Y) = −24,15/35,7 = −0,6764…

Y = cos ^-1 (−0,6764. ..)

Y = 132,5684…°

574 Y74 = 132,6° с точностью до одного десятичного знака.

Наконец, мы можем найти угол Z, используя «углы треугольника прибавляют к 180°»:

Z = 180° − 28,3881…° − 132,5684…°

Z = 19,0° к единице десятичный разряд

Вот еще один (немного более быстрый) способ решения треугольника SSS: сначала используйте закон косинусов, чтобы вычислить наибольший угол затем используйте закон синусов, чтобы найти другой угол и, наконец, используйте углы треугольника, добавленные к 180 °, чтобы найти последний угол.

Наибольший угол?

Почему мы пытаемся сначала найти наибольший угол? Таким образом, два других угла должны быть острыми (меньше 90°), и закон синусов даст правильные ответы.

Закон синусов трудно использовать с углами выше 90° . Может быть два ответа по обе стороны от 90° (пример: 95° и 85°), но калькулятор даст вам только меньшее значение.

Таким образом, если сначала вычислить наибольший угол с помощью закона косинусов, остальные углы будут меньше 90°, и закон синусов можно без труда использовать для любого из них.

Пример 3

B — наибольший угол, поэтому сначала найдите B, используя закон косинусов:

cos(B) = (a ² + c ² − b 90757 2 ) / 25ac 9007 cos(B) = (11,6 ² + 7,4 ² — 15,2 ² ) / (2 × 11,6 × 7,4)

COS (B) = (134,56 + 54,76 — 231,04) / 171,68

COS (B) = — 41.04) / 171,68

COS (B) = — 41.04) / 171,68

COS (B) = — 41.04) / 171,68

.

cos(B) = −0,2430…

B = 104,1° с точностью до одного десятичного знака

Используйте закон синусов, sinC/c = sinB/b, чтобы найти угол A:

sin(C) / 7,4 = sin(104,1°) / 15,2

sin(C) = 7,4 × sin(104,1°) / 15,2

sin(C) = 0,4722.